275
1
4
7
10
13
16
19
22
25
Р1
Р9
0
5
10
15
20
25
температура
длина
слой
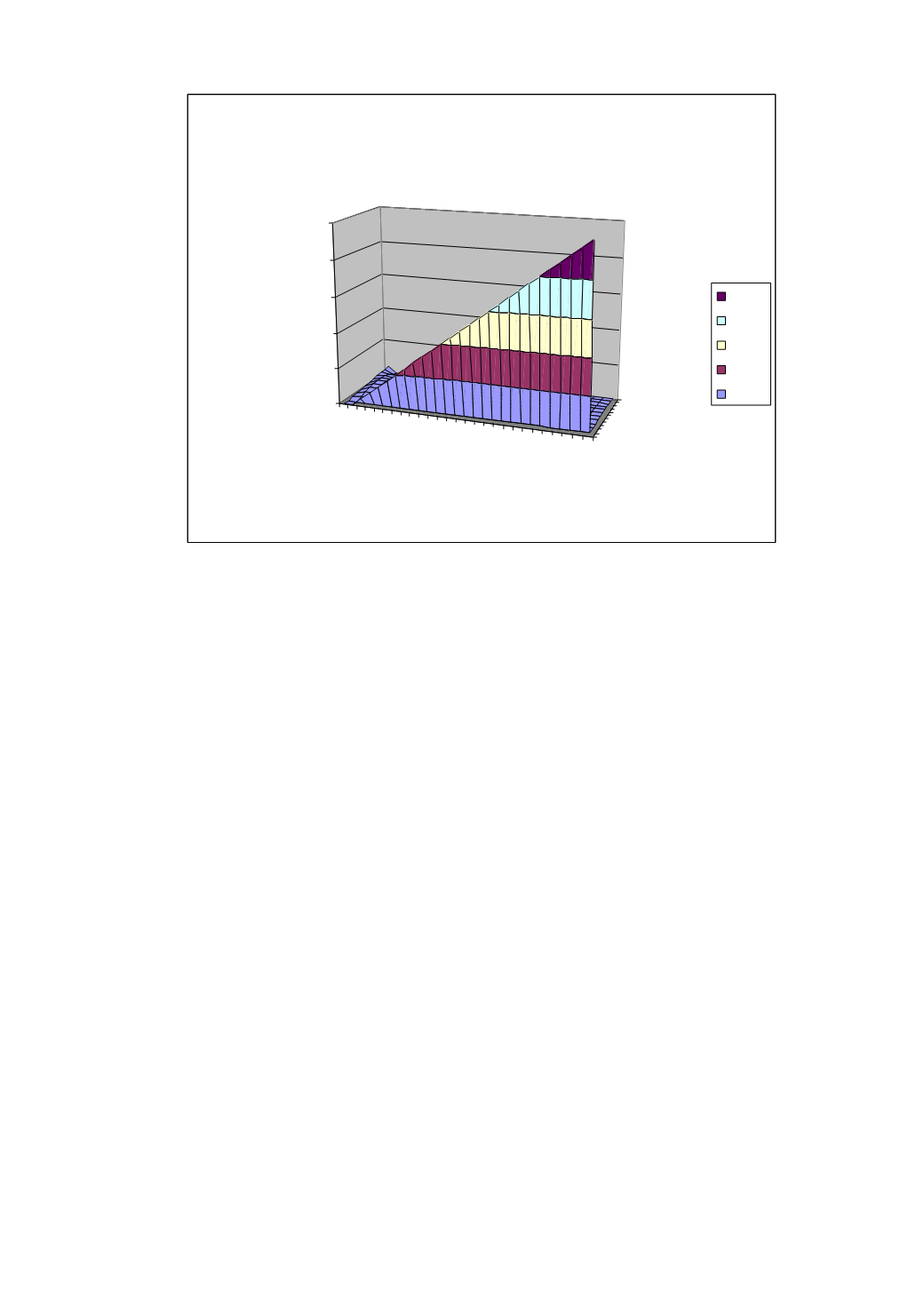
Уравнение теплопроводности
20-25
15-20
10-15
5-10
0-5
Рис. 9.8. Диаграмма
9.5. Использование метода сеток для решения
эллиптических уравнений
Рассмотрим эволюционную задачу для параболического уравнения с
краевыми условиями
.
0), (
) ,( ), (
)0,(
;
0),
(
) ,( ), (
)
,0(
;
0,
0), ,(
4
3
2
1
a x
x
bxux
x
u
b y
y
yauy
y
u
b y a x
yxf
u u
yy
xx
и произвольно заданными начальными условиями
). ,(
)0, ,(
;
0,
0), (
)
, ,( ), (
),0,(
;
0,
0), (
)
, ,( ), (
), ,0(
;
0,
0
,
0), ,(
0
4
3
2
1
yx
yxu
T t
a x
x
tbxux
t xu
T t
b y
y
tyau
y
ty u
T t
b y a
x
yxf
u u u
yy
xx
t
Если начальные и краевые условия задач таковы, что их решения
имеют
в
прямоугольнике
b y a x
yx
0,
0:) ,(
непрерывные
производные, равномерно ограниченные по
t
, то при
t
решение
нашей задачи равномерно сходится по
t
к решению стационарной задачи.
Физический смысл этого утверждения заключается в следующем: задача
описывает изменение с течением времени температуры в точках
прямоугольной области при заданных температурах в начальный момент
времени и постоянных значениях температуры на границе


