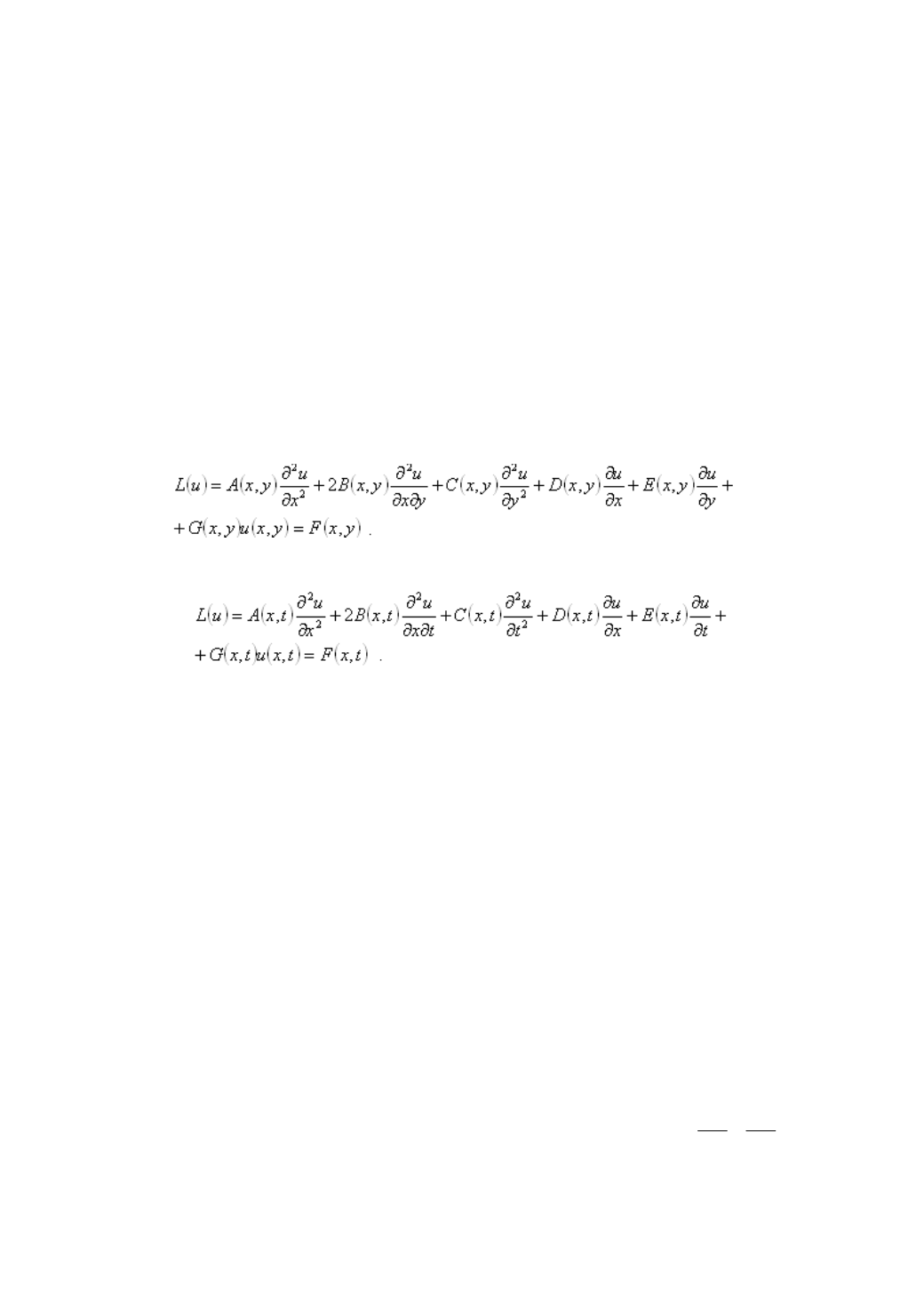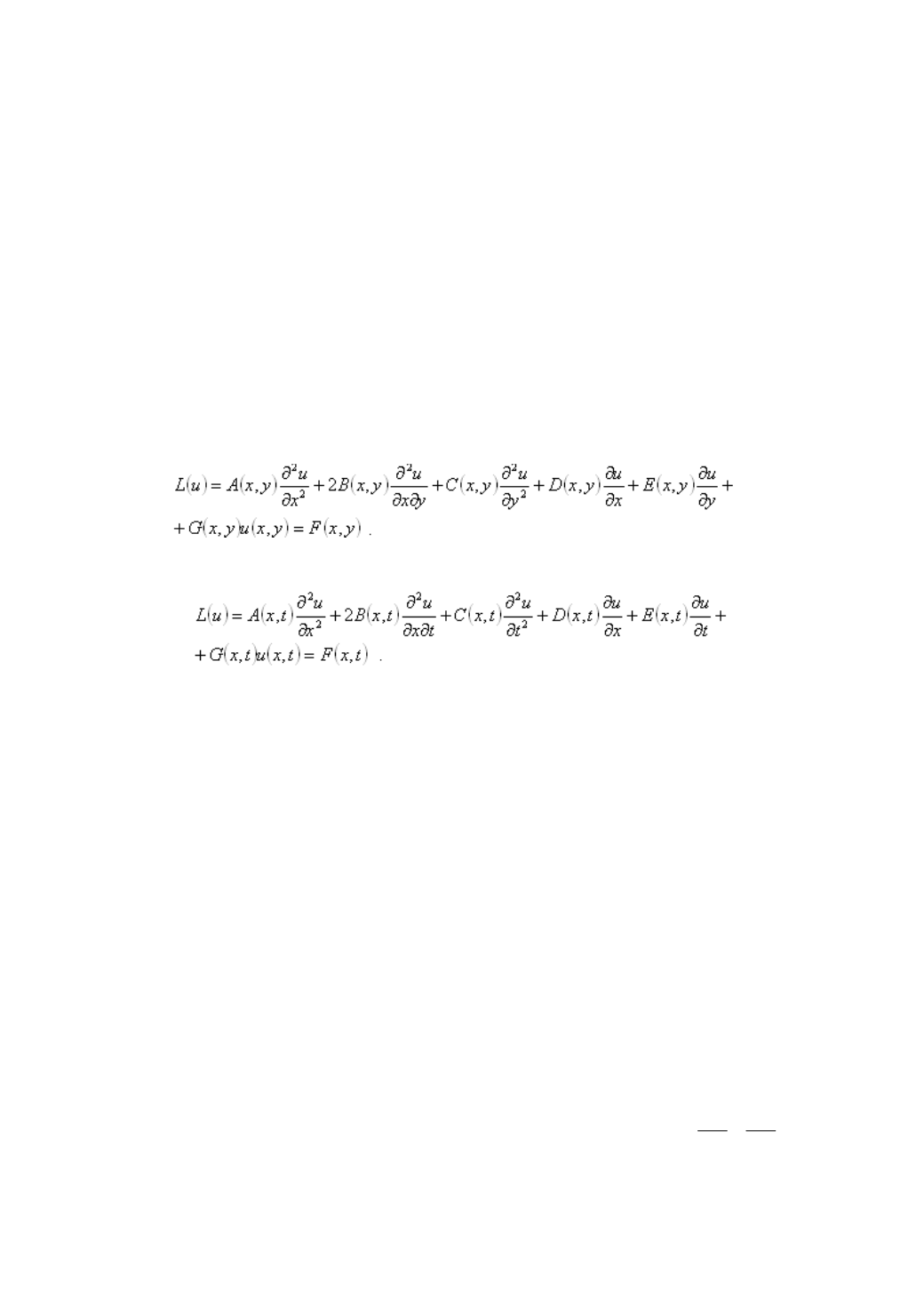
260
уравнениями с частными производными
, их часто называют уравнениями
математической физики.
К
решению
дифференциальных
уравнений
с
частными
производными приводят многие задачи механики и сплошных сред. Здесь
в качестве искомых функций обычно служат плотность, температура,
напряжение и др., аргументами которых являются координаты
рассматриваемой точки пространства, а также время. Универсальным
методом решения задач математической физики оказался метод конечных
разностей – метод сеток, позволяющий сводить приближенное решение
нелинейных уравнений в частных производных к решению систем
конечного порядка линейных алгебраических уравнений.
Линейным уравнением в частных производных второго порядка
называется соотношение между функцией
u
(
x
,
y
) (или
u
(
x
,
t
)) и ее
частными производными вида:
(9.1)
Если переменная функция
u
зависит от
х
и
t
, то уравнение (9.1) может
быть записано следующим образом:
(9.2)
В случае, если в правой части уравнения
F
=0
, то уравнения (9.1) и
(9.2) называются однородными, иначе неоднородными.
В зависимости от знака дискриминанта
AC
BD
4
2
уравнение может
принадлежать к одному из трех классов:
гиперболическому (
D
>0
);
параболическому (
D
=0
);
эллиптическому (
D
<0
).
В случае, когда
D
не имеет постоянного знака, то это уравнение
смешанного типа.
С помощью преобразования переменных
x
,
y
(или
x
,
t
) уравнение
можно привести к виду, когда
В
=0
. В этом случае очень просто
определяется тип уравнения. Если
А
и
С
имеют один и тот же знак, то
уравнение (9.2) эллиптическое, если разные, то гиперболическое, а если
А
и
С
равны 0, то уравнение относится к параболическим.
К классическим
эллиптическим
уравнениям относятся:
уравнение Лапласа
0
u
, которое используется для описания
магнитных и стационарных тепловых полей (
2
2
2
2
y
u
x
u
u
- в
двумерном случае);