" Н а у к а м о л о д ы х " , 2 6 н о я б р я 2 0 1 9 г . , А р з а м а с
П о с в я щ а е т с я 8 5 - л е т и ю в ы с ш е г о п е д а г о г и ч е с к о г о о б р а з о в а н и я в А р з а м а с е и
8 0 - л е т и ю п р о ф е с с о р а В я ч е с л а в а П а в л о в и ч а П у ч к о в а
454
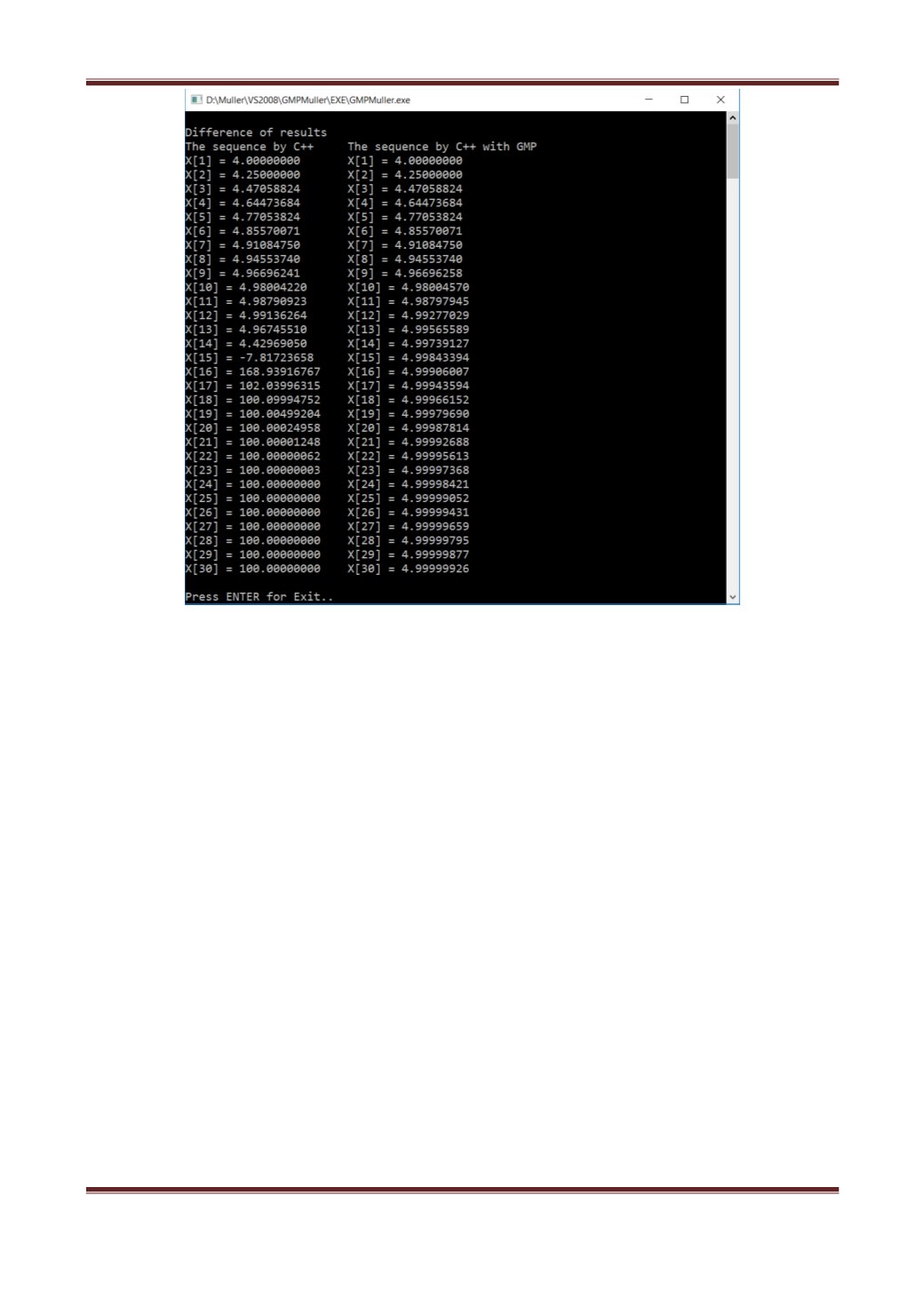
Рис.4. Результат работы программы на C++ с использованием GMP
Как видно из представленного листинга, последовательность сходится к
правильному ответу 5.
Вычисления с плавающей запятой всегда содержат риск потери точности.
Соотношение Мюллера яркий пример искусственно созданной задачи, где
стандарт хранения вещественных чисел IEEE 754 приводит к неправильному
решению. Использование специализированных библиотек, программного
обеспечения с целочисленной арифметикой позволяет решить данную
проблему. Тем не менее, на практике такое решение не всегда подходит по тем
или иным причинам ввиду лицензионных ограничений, проблем с замедлением
скорости вычислений и иных обстоятельств. Более того, последовательность
Мюллера это последовательность рациональных чисел, которое является
подмножеством множества вещественных чисел. Поэтому невозможно
предусмотреть заранее все возможные проблемы в будущем.
Чтобы минимизировать вероятность возможных ошибок, следует
тщательно выбирать модель, описывающую задачу проблемной области, знать
архитектуру вычислительной машины, критически подходить к средствам
разработки приложения, исследовать и анализировать полученные результаты,
подтверждать их корректность, сравнивая их с аналитикой, с другими
расчѐтами, экспериментальными данными. Это очень важно, поскольку,


