ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
92
Для изотермического процесса из уравнения состояния следует,
что при
T
1
=
T
2
=
T
P
1
V'
1
=
P
2
V'
2
=
RT
= const .
(5.45)
Изменение внутренней энергии равно нулю.
∆
U
=
C
V
(
T
1
–
T
2
) = 0.
(5.46)
Количество подведенной теплоты численно равно работе расширения
или сжатия
dq
=
dl
=
P
⋅
dV'
.
(5.47)
Работа расширения
l
при
Т
= соnst подсчитывается следующим образом:
∫
∫
=
=
=
=
2
1
2
1
) /
ln(
)'
/ '
ln(
'
/'
'
1 2
1
2
V
V
V
V
PP RT VV RT V RTdV
PdV l
(5.48)
Изменение энтропии определяется по зависимости
dS
=
dq
/
T
=
PdV'
/
T
=
RdV'
/
V'
,
∆
S
=
R
ln(
V'
2
/
V'
1
) =
R
ln(
P
1
/
P
2
) .
(5.49)
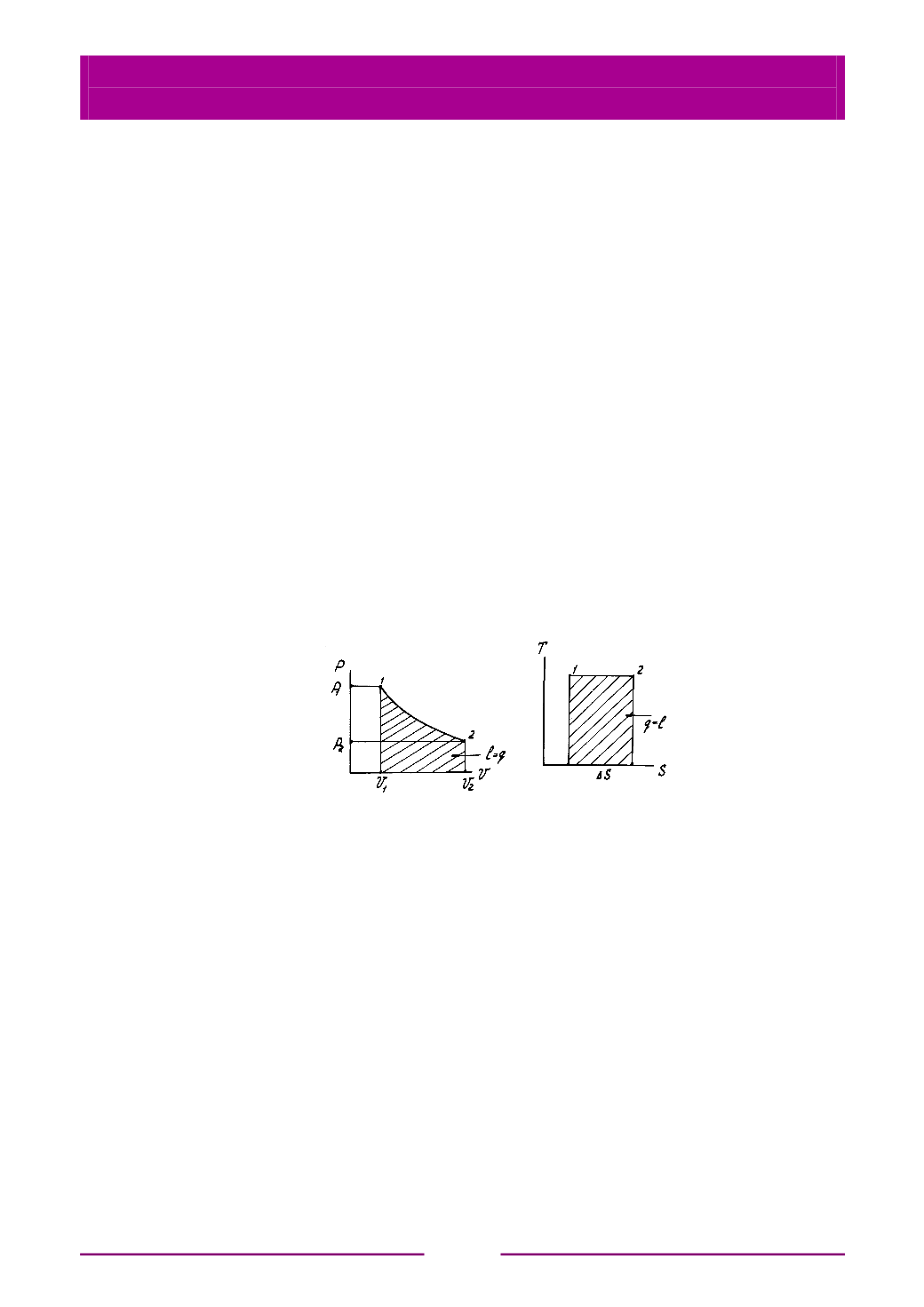
Изображение процесса
Т
= соnst в
РV
- и
TS
-координатах дано на рис. 5.7.
Рис. 5.7. Изображение изотермического процесса
в
PV
- и
ТS-
координатах
Из всех рассмотренных термодинамических процессов изотермический
может быть реализован для газа с определенным приближением. Используется
он в качестве эталонного в теории компрессорных машин, в циклах тепловых
двигателей и в других аналогичных случаях.
Для адиабатного процесса физическая сущность заключается в том, что он
протекает при отсутствии теплообмена между внешней средой и рабочим телом
q
= 0 и
dq
= 0. При
q
= 0 изменение энтропии
0 /
2
1
=
=
∫
Tdq
dS
. Отсюда следует, что
адиабатный процесс протекает при постоянной энтропии –
S
= const. Это дает
основание для наименования обратимого адиабатного процесса изоэнтропным.
Для вывода уравнения адиабатного процесса решим совместно два
адекватных уравнений (5.21) и (5.22) при условии
dq
= 0:
dq
=
C
V
dT
+
PdV'
= 0 и
dq
=
C
P
dT
–
V'dP
= 0.


