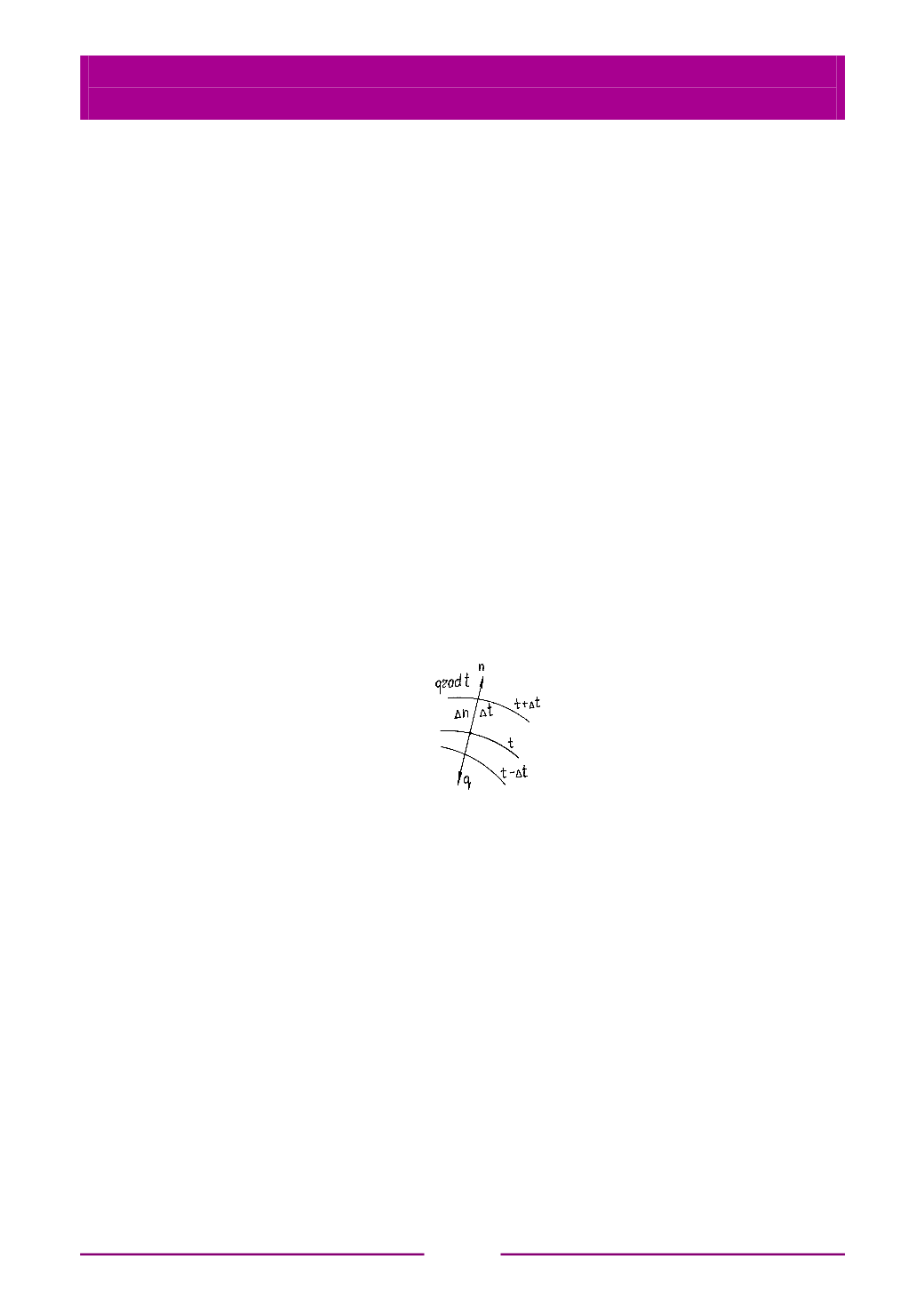
ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
98
t
= (
x
,
y
,
z
,
τ
).
(6.1)
Совокупность температур в различных точках пространства называется
температурным полем, а линии, соединяющие точки с одинаковыми
температурами, изотермами. Если температура изменяется во времени, то мы
имеем дело с нестационарным температурным полем. Если температура
меняется только в пространстве и не зависит от времени, то такое
температурное поле называется стационарным.
Исходя из зависимости температуры от координат точек различают три
вида температурных полей: трехмерное
t
=
f
(
x
,
y
,
z
), двухмерное
t
=
f
(
x
,
y
) и
одномерное
t
=
f
(
x
). Наиболее простые закономерности возникают при
изучении одномерного поля. Исходя из этого их используют с определенной
степенью приближения и для двухмерных и трехмерных полей. Остановимся
также на понятии температурного градиента.
Как видно из рис. 6.1, наибольшее изменение температуры протекает в
направлении нормали к изотермическим поверхностям. В этой схеме градиент
температуры
n t
n t
t
n
∂ ∂=∆∆ =
→∆
/
] / [ lim
0
grad
является вектором, имеющим
размерность К/м . Не следует, как это часто делают, смешивать понятия
градиента grad
t
и перепад
∆
t
температур. Величины эти имеют разные
физический смысл и размерности.
Рис. 6.1. Градиент температур
За положительное направление вектора градиента принимается направление
возрастания температуры, от меньшего к большему ее значению. Плотность
теплового потока
q
является также вектором. Однако положительное
направление считается в сторону убывания температуры, от большего к
меньшему значению.
Закономерности теплопроводности, в первую очередь, определяются
законом Фурье
q
= -
λ
grad
t
.
(6.2)
Как показано выше, векторы
q
и grad
t
имеют противоположное
направление и разные знаки. Коэффициент пропорциональности называется
коэффициентом теплопроводности. Размерность его – Вт/(м
⋅
К). Из сказанного
следует, что коэффициент теплопроводности
λ
– это плотность теплового
потока при прохождении его через один метр расстояния между исходными
точками, имеющими разность температур в один градус.