М а т е р и а л ы X I I В с е р о с с и й с к о й н а у ч н о - п р а к т и ч е с к о й к о н ф е р е н ц и и
П о с в я щ а е т с я 8 5 - л е т и ю в ы с ш е г о п е д а г о г и ч е с к о г о о б р а з о в а н и я в А р з а м а с е и
8 0 - л е т и ю п р о ф е с с о р а В я ч е с л а в а П а в л о в и ч а П у ч к о в а
469
ОБ УСТОЙЧИВОСТИ КОЛЕБАНИЙ ПЕРЕВЕРНУТОГО
ДВОЙНОГО МАЯТНИКА
Чурилова Н.Э.
магистрант, Арзамасский политехнический институт (филиал) НГТУ
им. Р.Е.Алексеева, г. Арзамас
Научный руководитель Маслов И.Н., к.ф.-м.н., доцент
Аннотация.
Рассмотрено
движение
перевернутого
двойного
математического маятника вблизи верхнего положения равновесия. Система
дифференциальных уравнений, определяющих колебания маятника, была
проинтегрирована численно при наличии вертикальных вибраций оси
маятника. Показано, что при некоторых значениях амплитуды и частоты
вибраций движение маятника стабилизируется вблизи верхнего положения
равновесия и остается устойчивым в течение промежутка времени, в
несколько десятков раз превышающего период собственных колебаний
маятника.
Ключевые слова: двойной маятник, верхнее положение равновесия,
уравнения Эйлера-Лагранжа, вибрационный момент, устойчивость колебаний.
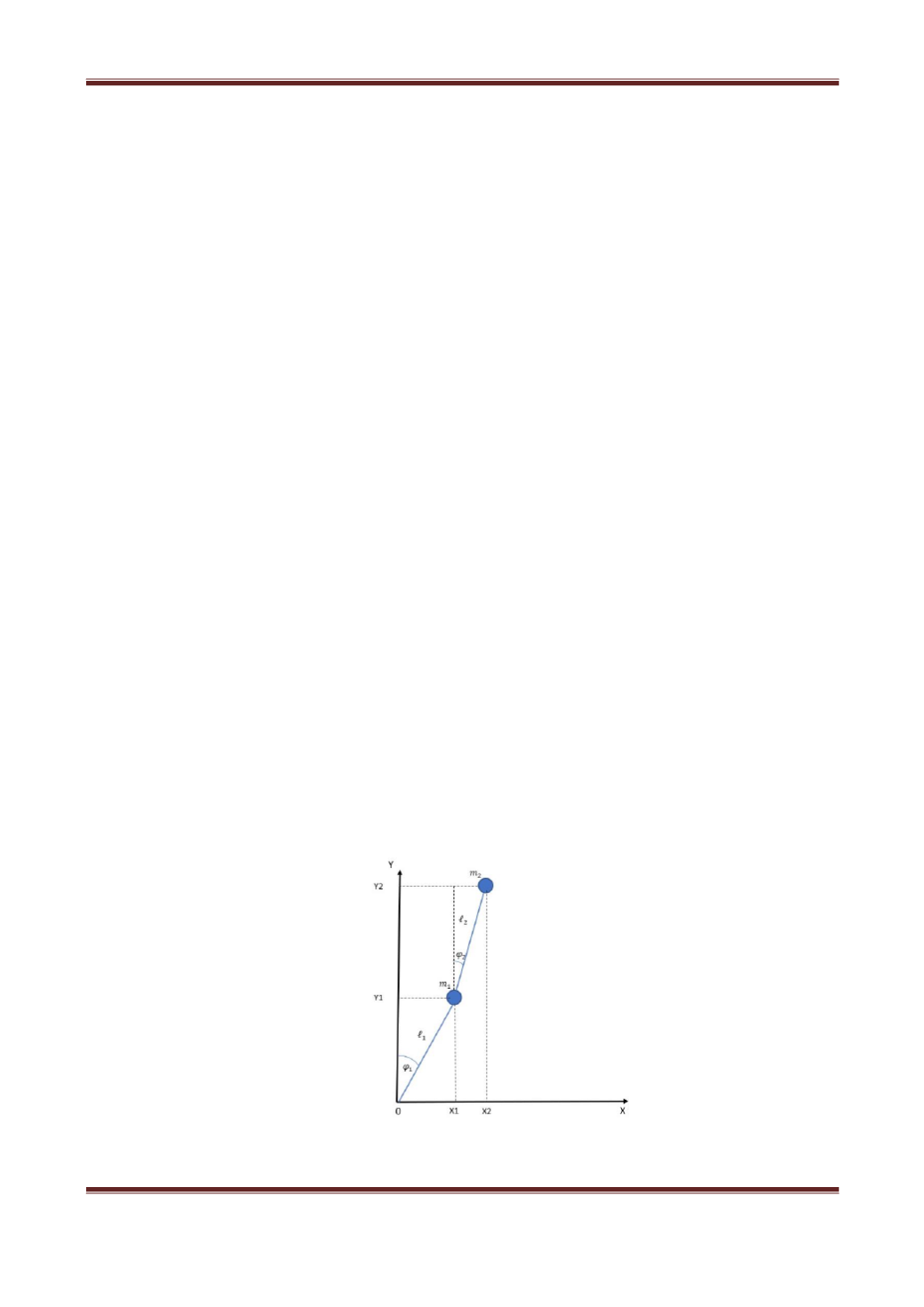
Двойной маятник, несмотря на внешнюю простоту своего устройства,
представляет собой систему, обладающую способностью совершать
чрезвычайно сложные движения. В отличие от простого маятника, колебания
которого имеют понятный и регулярный характер, движения двойного
маятника приобретают качественно новые черты; хотя уравнения его движения
являются детерминированными, и существуют такие значения параметров
системы, при которых движения маятника оказываются хаотическими.
Двойной маятник представляет собой систему с двумя степенями
свободы, которая получается в результате соединения двух маятников
посредством различных связей (в частности, твердых, упругих,
электромагнитных и т.п.).
Рис.1. Двойной перевернутый маятник


