" Н а у к а м о л о д ы х " , 2 6 н о я б р я 2 0 1 9 г . , А р з а м а с
П о с в я щ а е т с я 8 5 - л е т и ю в ы с ш е г о п е д а г о г и ч е с к о г о о б р а з о в а н и я в А р з а м а с е и
8 0 - л е т и ю п р о ф е с с о р а В я ч е с л а в а П а в л о в и ч а П у ч к о в а
270
где
Mкр
- крутящий момент;
G
- модуль сдвига;
Jx
- осевой момент инерции площади поперечного сечения (рис. 2).
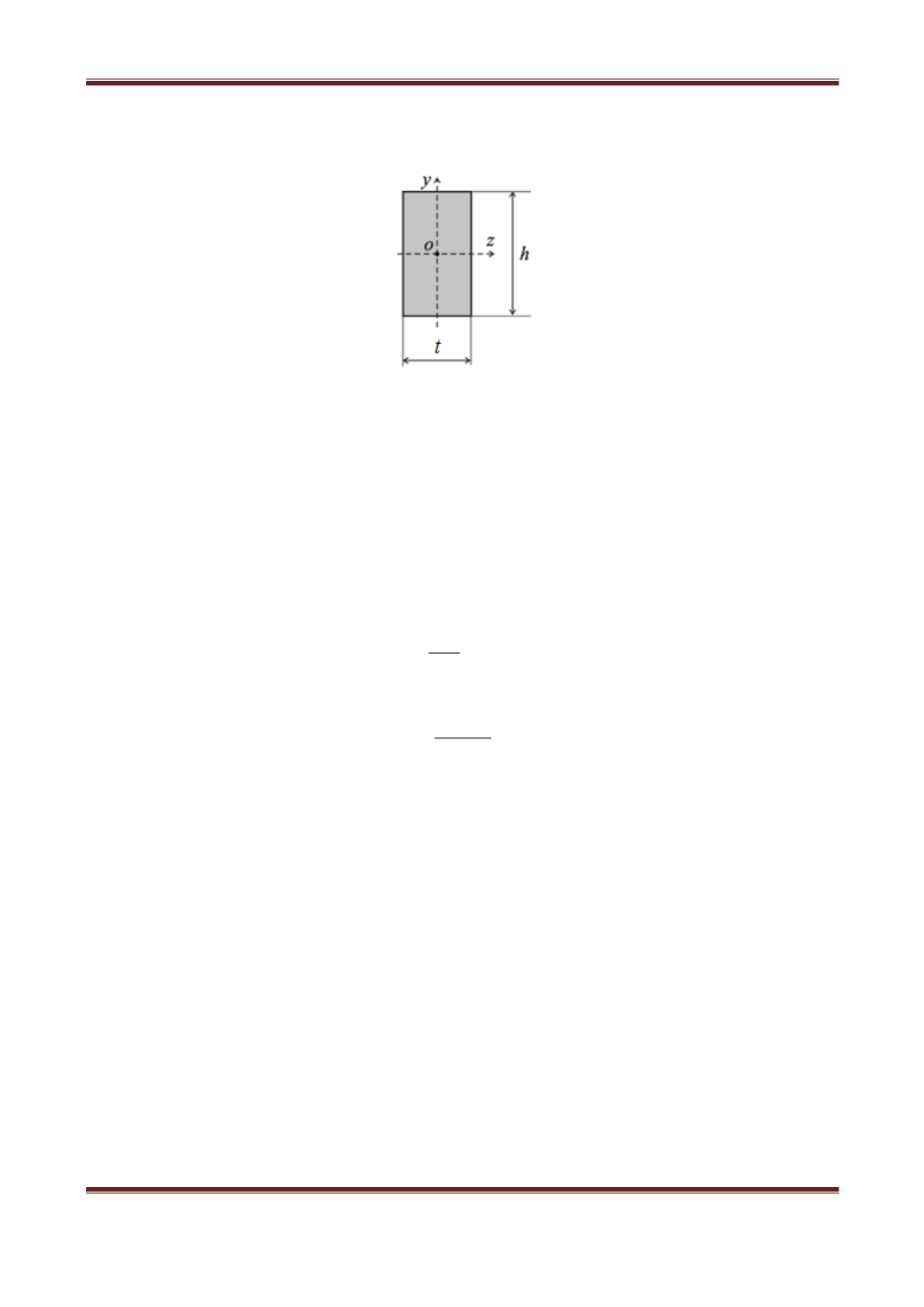
Рис. 2. Сечение торсиона в первом приближении
Геометрическая форма торсиона является важнейшей характеристикой
при расчѐте жѐсткости и определяет выбор метода расчета. Разные формы
сечений имеют различные геометрические характеристики - числовые
величины (параметры), определяющие размеры, форму, расположение
поперечного сечения однородного по упругим свойствам деформируемого
элемента конструкции (характеризующие сопротивление элемента различным
видам деформации).
Сечением торсионов является прямоугольник, для которого:
12
3
ht
J
x
. (3)
Используя размеры сечения, t=1.8 мм, h=9 мм, получим
4,4
12
8.19
3
x
J
мм4.
Это для одного торсиона, а их 12 для двух виброподвесов. Тогда для
обоих виброподвесов осевой момент инерции площади поперечного сечения
составит Jx=53 мм4.
Задачей ставится определить толщину торсиона вибрационного подвеса
для достижения оптимальных кинематических параметров. Критерием
оптимальности является максимум угловой скорости при максимальной частоте
колебаний.
Данная задача может быть решена изменение геометрических
характеристики упругих торсионов за счѐт варьирования величины осевого
момента инерции площади поперечного сечения. Более рационально изменять
толщину торсионов, так как в этом случае, согласно выражению (3), момент
инерции Jx, а, следовательно, их жѐсткость и жесткость виброподвесов в целом
изменяется в кубической зависимости. Проведѐм исследования с
использованием SolidWorksSimulation [2]. Для решения необходимо знать хоть
одно начальное условие, например, амплитуду колебаний, которую можно
взять с макетного образца. Далее при помощи инструмента «Исследование


