88
интервала, т.е. равна, например, ∆
dt
. В этом случае вероятность
Р(N)
полу-
чить за какой-то фиксированный промежуток времени
t
то или иное число
событий
N
определяется законом Пуассона. (Вывод см. в работах [1] ,[5]).
!
e) ( ) (
0
0
N
N NP
N N
−
=
(1)
где
N
o
- среднее число событий за время
t
.
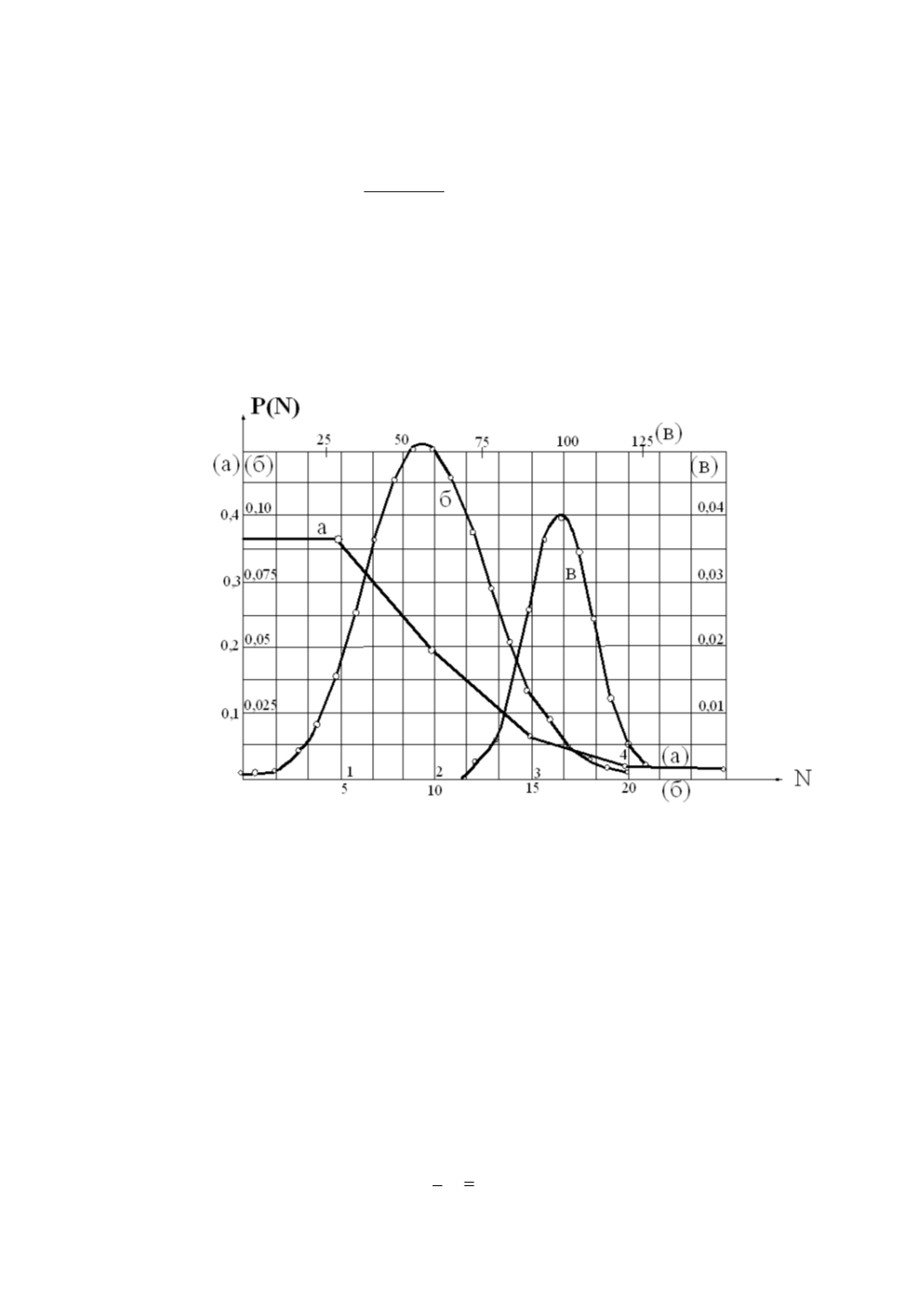
Для иллюстрации закона Пуассона на рис. 56 приведены графики для
трех различных значений
N
о
: a)
N
о
= 1, б)
N
о
= 10, в)
N
о
= 100. Следует иметь
в виду, что на этих графиках имеет смысл только значения
Р(N)
для целых
N
. Соединены же соответствующие точки плавными линиями просто для
большей наглядности.
Приведенные графики и непосредственные вычисления по формуле (1)
показывают, что за выбранный промежуток времени в отдельном измере-
нии может иметь место любое число событий - от нуля до сколько угодно
большого, при этом:
1) наиболее вероятным являются числа
N = N
o
и
N = N
o
1;
2) с увеличением
N
o
уменьшается относительная ширина распределе-
ния Пуассона, т.е. ширина области значений
N
, для которых вероятность
появления еще существенна-не очень мала по сравнению с
P(N
o
).
Действи-
тельно, мерой отклонения случайно величины от ее среднего значения явля-
ется, как известно, дисперсия
D
или связанная с ней величина–стандартное
отклонение σ:
2
2
( ) ( ) (
)
D N N N N
⋅ σ = −
.
(2)
Рис. 56


