85
Приложения
1. Метод наименьших квадратов
При обработке экспериментальных данных часто возникает задача об
их согласовании, с какой-то теоретической функцией. При этом обычно тре-
буется путем согласования с опытом определить значения констант, входя-
щих в эту теоретическую функцию.
Простейшим примерок задачи такого рода является исследование зави-
симости между двумя измеряемыми величинами
х
и
у
. Результаты экспери-
ментального исследования такой зависимости можно представить в виде пар
чисел
(х
1
, у
1
), (х
2
, у
2
)
(^ , ^) …
(х
n
, у
n
),
в каждой из которых величины
х
i
и
у
i
, в
общем случае, определены с соответствующими погрешностями σ
хi
и σ
уi
.
Однако в нашей роботе мы ограничимся рассмотрением более простого, но
довольно часто встречающегося на практике случая, когда точность измере-
ния величин
х
i
во много раз превышает точность измерения величин
у
i
и
можно принять, что все σ
хi
=0. В этом случае экспериментальные данные
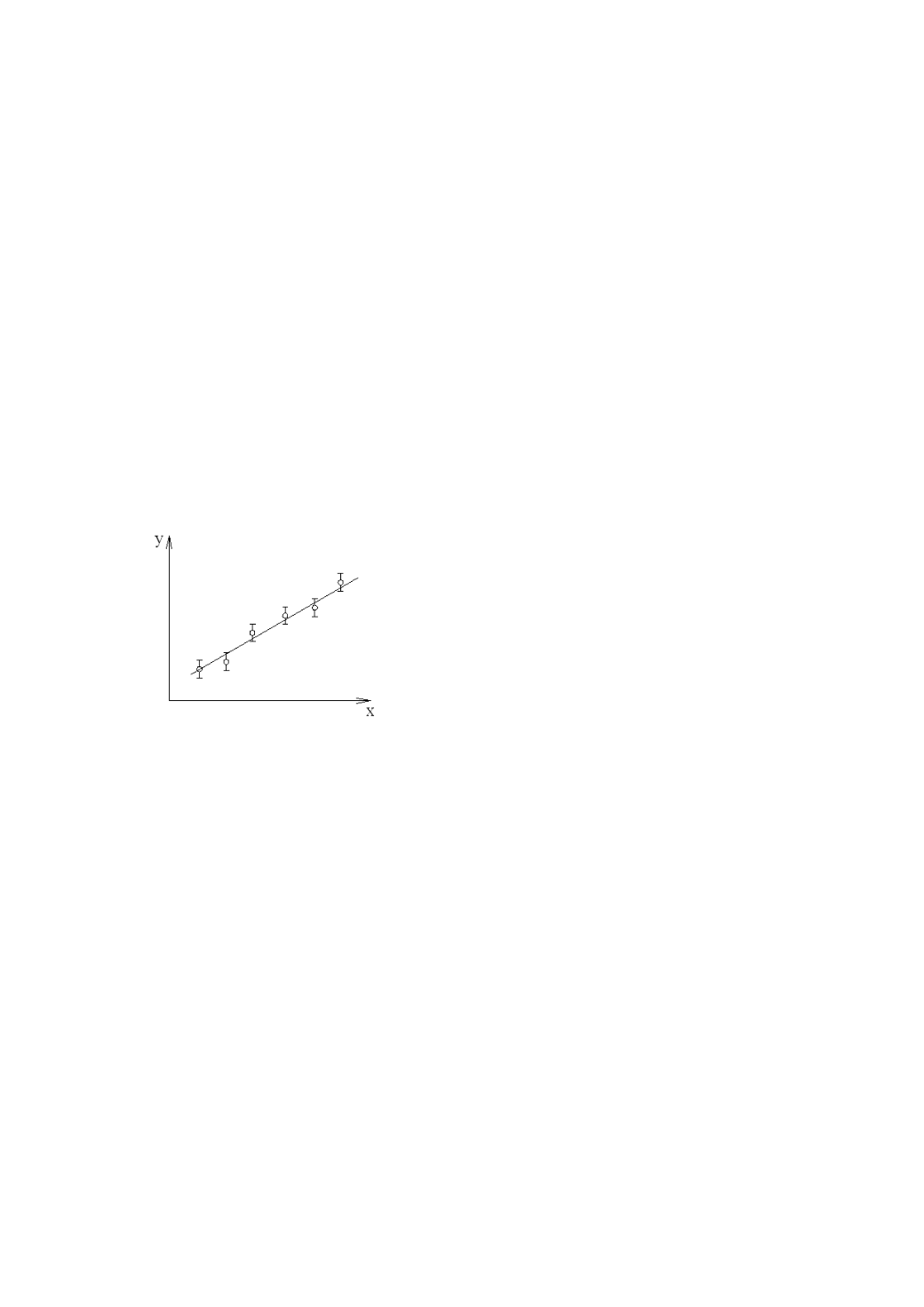
можно представить графически так, как это изображено на рис. 55. Пусть
нам известно также, что зависимость между
х
и
у
должна быть линейной,
т.е.
у=а+bх
. Спрашивается, как же выбрать
константы
а
и
b
, чтобы прямая проходила в
наилучшем согласии с экспериментальными
точками? Естественно, что искомая прямая
должна пройти так, чтобы все эксперимен-
тальные точки лежали возможно ближе к
ней. При этом, очевидно, прямая должна
проходить как можно ближе к тем точкам,
которые измерены с наиболее высокой точ-
ностью (с малой погрешностью σ
уi
).
Также ставится задача, если через экс-
периментальные точки нужно провести не прямую, а параболу или какую-то
другую кривую, функциональное выражение которой задано.
Такие задачи обычно решают с помощью предложенного Лежандром
метода наименьших квадратов, сущность которого применительно к нашему
случаю можно сформулировать следующим образом: неизвестные парамет-
ры (константы) функции, приводимой в соответствие с экспериментальными
данными, должны быть выбраны так, чтобы сумма квадратов уклонения от
нее экспериментальных точек была минимальна.
2
2
(
)
i
i
i
i
S
у у
= ε = −
∑ ∑
(7)
Сформулированный принцип позволяет не только найти значения инте-
ресующих констант, но и оценить точность, с которой они определяются из
данной серии измерения. Однако, прежде чем перейти к конкретным фор-
мулам, еще более упростим нашу задачу, предположив, что искомая линей-
ная зависимость и изображается уравнением
у=bх
(т.е.
а
=0 и, искомая пря-
мая проходит через начало координат), и что измерения всех величин
у
i
вы-
полнены с одинаковой точностью σ
уi
=const (равноточные измерения).
Рис. 55


