107
щих электронов (
E
), а в случае непрерывного спектра β-частиц функцией
максимальной энергии, т.е.
обр
( , , )
q F Z d E
=
.
Рассмотрим зависимость коэффициента обратного рассеяния от этих
трех величин.
1. Зависимость вероятности обратного рассеяние от атомного номера
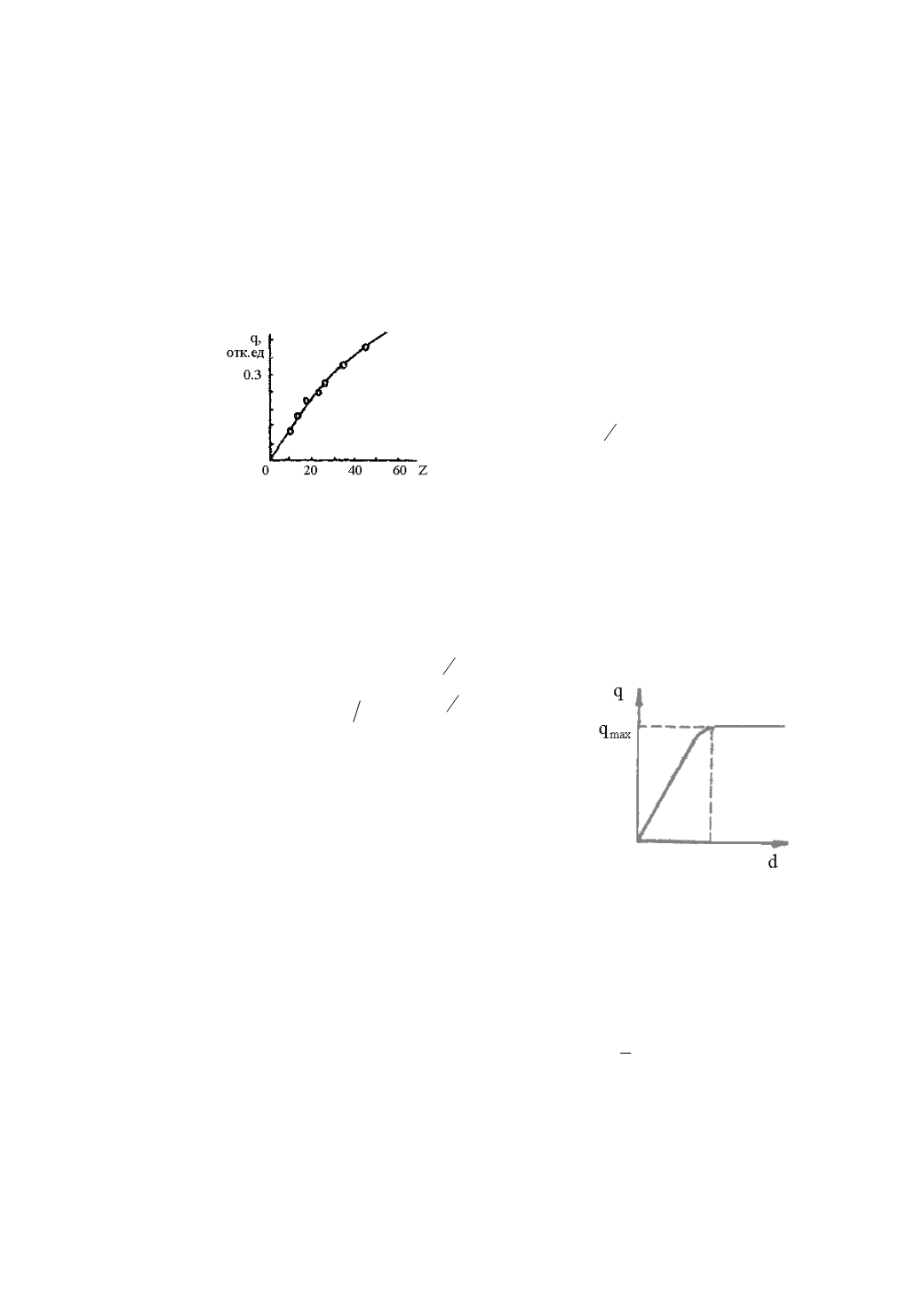
отражателя. На рис. 67 приведена типичная экспериментальная зависимость
q(Z)
в случае отражения β-частиц, испущенных радиоактивным препаратом
32
P (
E
βmax
=1,71 МэВ). Толщины ма-
териалов взяты заведомо больше,
чем толщины обратного насыщения
(см. п. 2). Экспериментальная кри-
вая, показана на рис.67, удовлетво-
ряет аналитической зависимости
2
3
( )
q Z B Z
= ⋅
, где B-коэффициент,
зависящий от геометрических усло-
вий опыта, в частности от телесного
угла окна счетчика. Здесь следует
отметить, что обратно-рассеянное
излучение не изотропно – его максимальная интенсивность наблюдается в
направлении, перпендикулярном плоскости отражателя. Максимальная
энергия и максимальный пробег отраженных электронов также зависит от
Z
.
Например, в случае излучателя
32
P
:
1
3
отр.max
(
) 0.24
E МэВ
Z
=
,
1
2
2
отр.max
(
) 48
R мг см Z
=
.
2. Если увеличивать толщину отражателя
и измерять интенсивность потока обратно
рассеянных электронов, то сначала будет воз-
растать почти линейно (рис. 68), затем рост
замедлиться и далее
q
достигнет некоторого
предельного значения
q
max
.
Толщина слоя вещества, начиная с которой не
зависит от толщины отражателя, называется
толщиной насыщения обратного рассеяния
d
н
. Эта толщина равна примерно
1/5 от максимального пробега β-частиц данной энергии в данном веществе.
Например: максимальный пробег электронов, испущенных
32
P, равен 0,78
г/см
2
, т.е. соответствует толщине алюминиевой пластинки 0,29 см, следова-
тельно, толщина насыщения в алюминии равна
H
1 0.058
5
d
R
= ⋅ =
см.
Рис. 67
Рис. 68


