ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
73
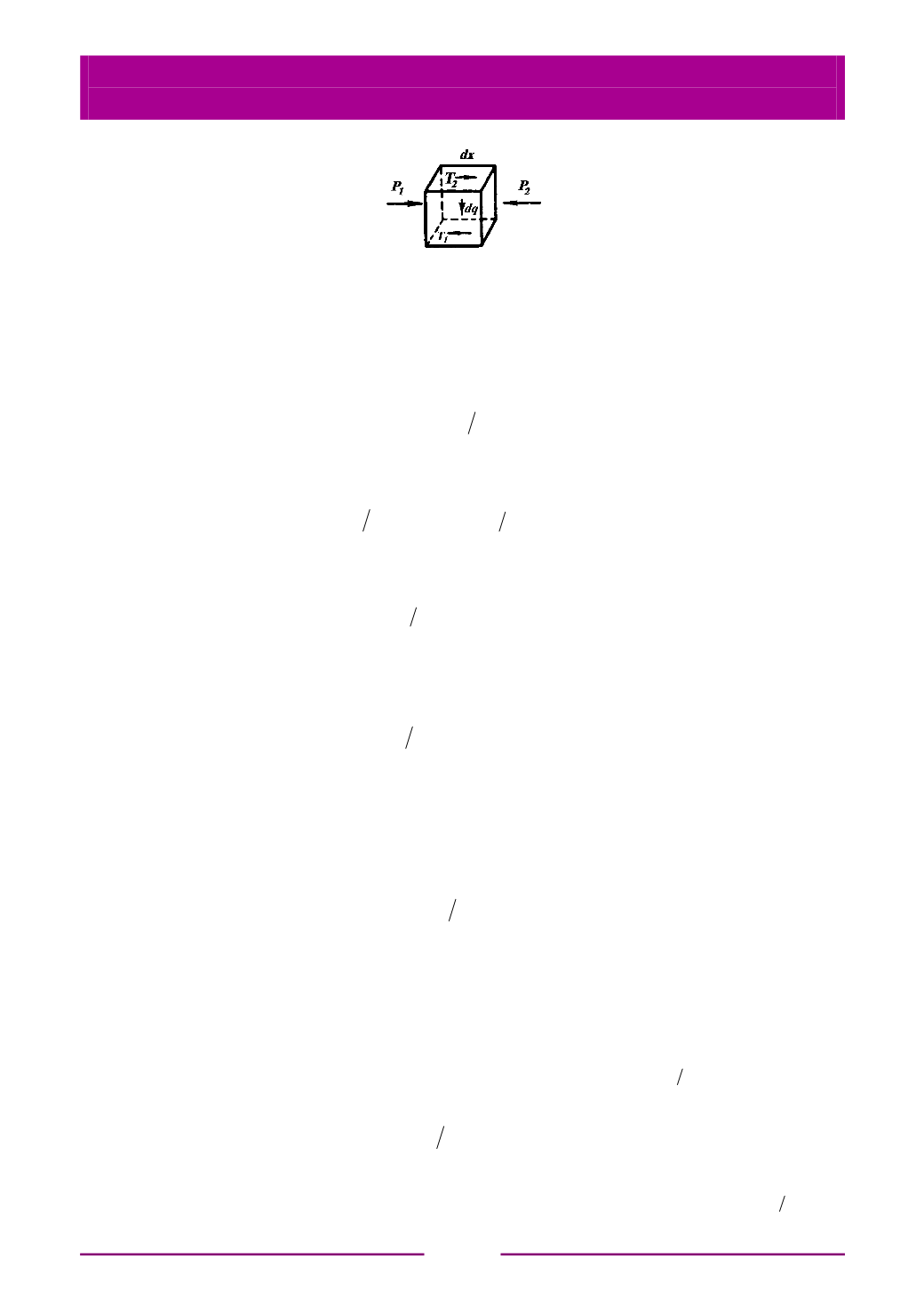
Рис. 4.2. Исходная схема к выводу
чисел гидродинамического подобия
Выделенный объем движется со скоростью
ω
. Масса элементарного
куба
dm
=
ρ
dx
3
.
Сила внутреннего трения
T
согласно уравнению (3.5) равняется
dx dx d TF
2
ω
µ
= =
.
(4.11)
Подставляя найденную величину в уравнение (4.7) и используя метод
приведения, получим
idem
Ne
=
→
=
x
d dxdx
dx dx d
ρω
µ
ω
ρ
ω
µ
2 3
2
.
(4.12)
Обратная величина полученного значения представляет собой уже
известное нам число Рейнольдса
idem
= =
ν
ω
l
Re
,
(4.13)
где
l
=
x
- определяющий размер.
Подставляя в (4.7) силу тяжести
F
=
m
g и произведя преобразования,
получим число подобия Фруда
idem
g Fr
=
=
2
ω
l
.
(4.14)
Если число Re является мерой отношения инерционных и вязкостных сил в
условиях движения жидкости или газа, то число Фруда представляет собой
меру отношения гравитационных и инерционных сил. Вместо числа Фруда
можно использовать число Галилея, которое равно произведению чисел Фруда
и Рейнольдса во второй степени.
idem
g
Fr
Ga
=
=
=
2 3
2
Re
ω
l
.
(4.15)
Число Галилея является мерой отношения гравитационных и вязкостных сил.
В практике проектирования и эксплуатации нагревательных устройств
определенное значение имеет число Архимеда. Оно учитывает действие
подъемной силы газов и жидкостей при их нагревании или охлаждении.
Число Аr получается в том случае, если в число Ga вместо ускорения силы
тяжести
g
подставить ускорение подъемной силы
ρ ρ−ρ =
)
(
o
g a
, где
ρ
и
ρ
0
-
плотности холодной и более нагретой сред.
(
)
idem
Ar
o
=
−
=
ρ
ν
ρ
ρ
2
3
l
g
.
(4.16)
Плотности газов и жидкостей, как известно, зависят от их температуры.
Коэффициент
объемного
расширения
идеальных
газов
, 1
T
=β
К
-1
.


