" Н а у к а м о л о д ы х " , 2 6 н о я б р я 2 0 1 9 г . , А р з а м а с
П о с в я щ а е т с я 8 5 - л е т и ю в ы с ш е г о п е д а г о г и ч е с к о г о о б р а з о в а н и я в А р з а м а с е и
8 0 - л е т и ю п р о ф е с с о р а В я ч е с л а в а П а в л о в и ч а П у ч к о в а
348
где
H
- кинетический момент гироскопа,
k
x
- крутизна моментного устройства.
В соответствии с показанной на рис. 2 системой координат, связанной с
основанием, уравнения движения гироскопа с учетом малости углов
отклонения ротора имеют вид:
изм
изм
2
изм
изм
2
y
x
x
y
x
y
x
y
y
x
y
x
A
H
M H
H K m
A
H
M H
H K m
(1)
где
и
– углы поворота ротора гироскопа относительно корпуса вокруг осей
x
и
y
;
А
– момент инерции карданного подвеса;
Н
– кинетический момент;
x
и
y
– угловые скорости корпуса гироскопа;
M
x
и
M
y
–внешние возмущающие моменты;
x
2
и
y
2
– углы отклонений осей датчиков вокруг оси собственного
вращения
z
;
2
1
K K J
– остаточная жесткость карданного подвеса;
m
η
- постоянная времени ДНГ, обусловленная газодинамическими
моментами.
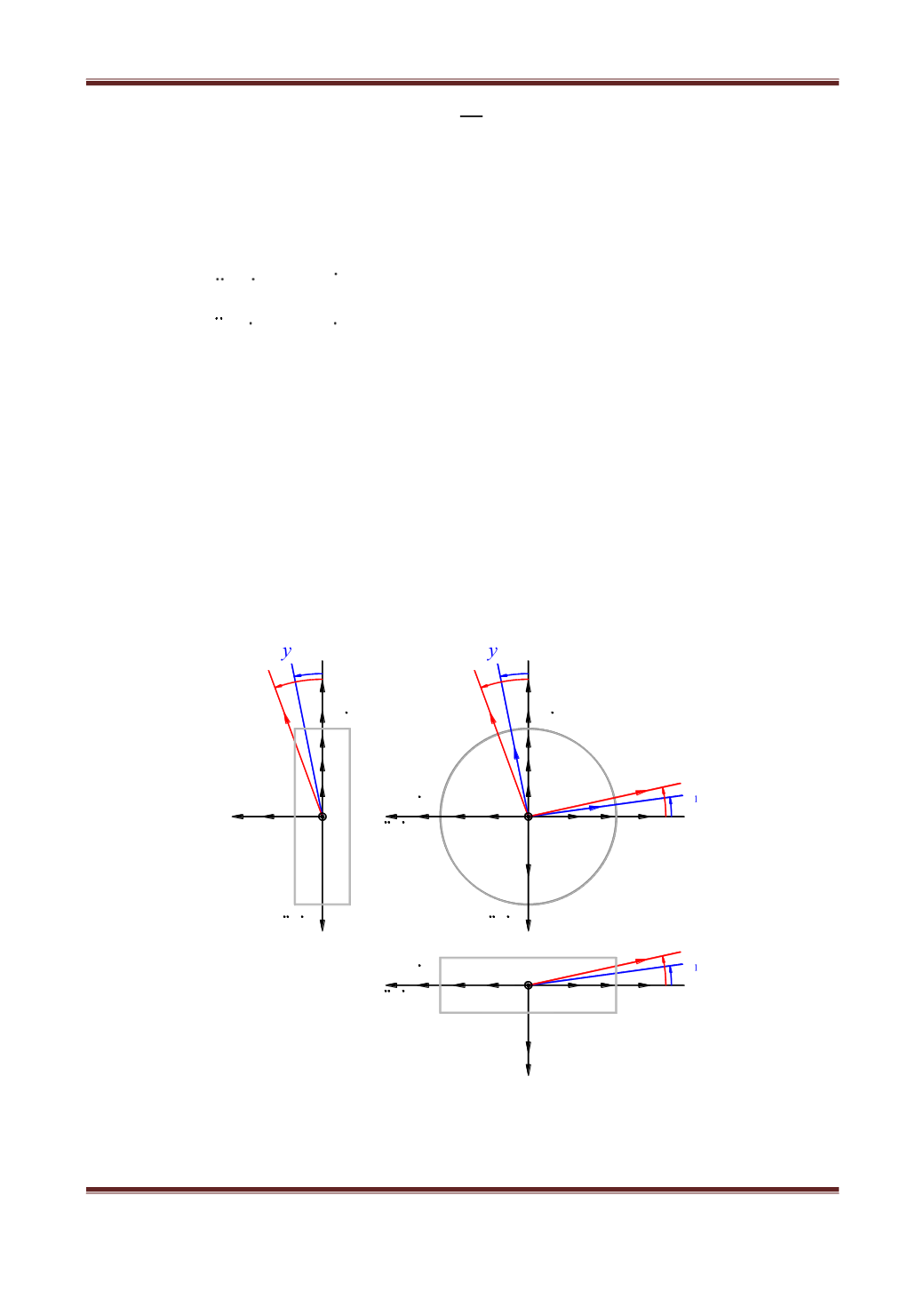
Рис. 2. Система координат
Анализ представленных уравнений движения показывает наличие
паразитной перекрестной связи между измерительными каналами. Например,
U
U
y
m
x
y
x
x
y
2
2
1
o
1
x
2
x
2
y
1
y
A
( )
x
y
A
( )
y
x
H
( )
y
H
( )
x
M
x
M
y
x
y
y
2
1
o
01
z
H
02
x
x
x
2
o
02
01
x
H
y
z
M
x
дм
M
y
дм
z
M
y
дм
M
x
дм
K
m
K
m
H
( )
x
M
y
A
( )
x
H
( )
y
M
x
K
m
A
( )
y


