ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
138
Сходимость схемы означает, что при сгущении сетки решение системы
алгебраических
уравнений
приближается
(сходится)
к
решению
дифференциального
уравнения
при
заданных
краевых
условиях.
Сходимость – следствие одновременных аппроксимируемости и устойчивости.
Для примера заменяем в дифференциальном уравнении (6.6)
теплопроводности бесконечно малые приращения приращениями конечной
величины и уравнение принимает вид:
t
(при
x
= const)/
∆τ
=
a
∆
2
t
(при
τ
= const)/
∆
x
2
(6.94)
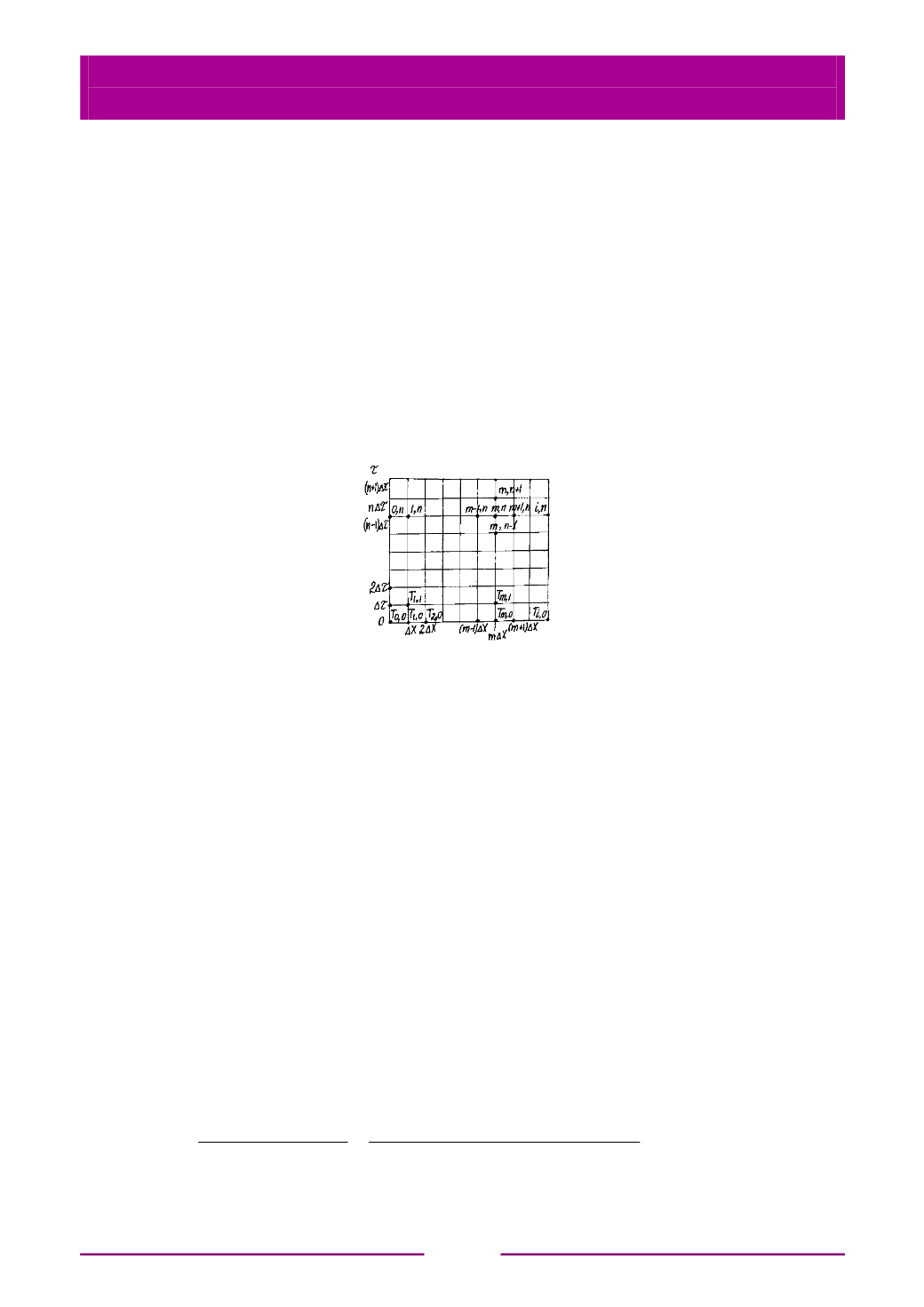
Нагреваемую или охлаждаемую пластину разделим на ряд слоев толщиной
∆
x
, м (рис. 6.33), а время процесса – на ряд периодов
∆τ
, ч.
Рис. 6.33. Схема распределения температур
к расчету методом конечных разностей
Тогда
t
n
∆τ
;
m
∆
x
будем обозначать температуру через
n
периодов от начала
процесса на расстоянии
m
∆
x
от поверхности пластины, принятой за начало
координат.
Пользуясь этой системой обозначений, получим изменение температуры на
расстоянии m
∆
х
от поверхности за время от
n
∆τ
до (
n
+ 1)
∆τ
∆
t
(при
x
= const) =
t
(
n
+1)
∆τ
;
m
∆
x
–
t
n
∆τ
;m
∆
x
.
(6.95)
Изменение температуры по толщине стенки для момента времени
n
∆τ
дает
∆
t
(при
τ
= const) =
t
n
∆τ
;(
m
+1)
∆
x
–
t
n
∆τ
;
m
∆
x
.
(6.96)
И, наконец,
∆
2
t
(при
τ
= const) =
t
n
∆τ
;(
m
+1)
∆
x
- 2
t
n
∆τ
;
m
∆
x
+
t
n
∆τ
;(
m
-1)
∆
x
.
(6.97)
Подставляя полученные выражения для
∆
t
и
∆
2
t
в основное уравнение
(6.94), будем иметь
(
)
2
)1 (;
;
)1 (;
;
; )1 (
2
x
t
t
ta
t
t
x m n xm n
x m n
xm n xm n
∆
+
−
=
∆
−
∆+ ∆
∆ ∆
∆+ ∆
∆ ∆
∆ ∆+
τ
τ
τ
τ
τ
τ
(6.98)


