ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
133
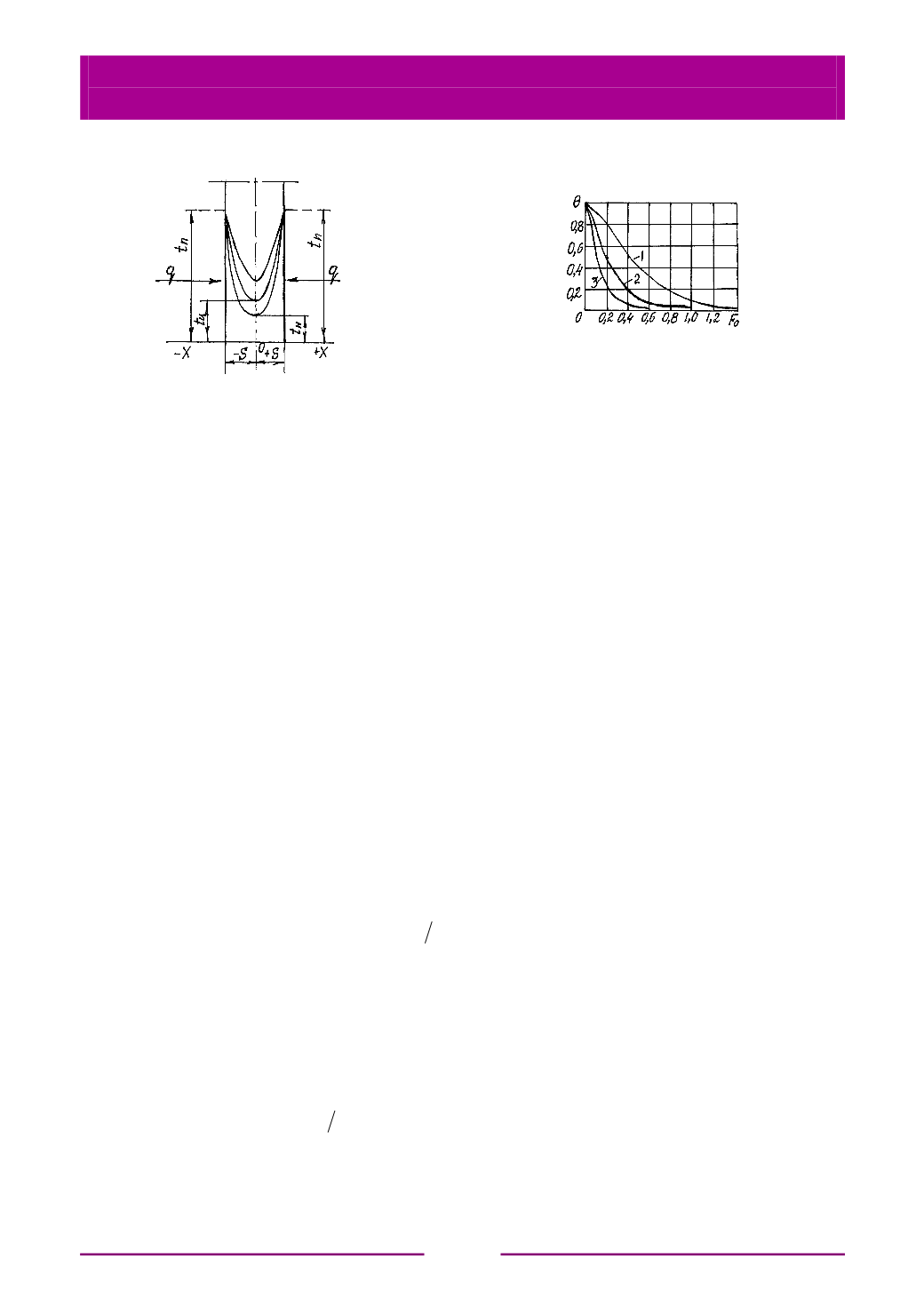
Рис. 6.26. Схема нагрева бесконечной
пластины при мгновенном повышении
температуры ее поверхности
Рис. 6.27. Измерение относительной
температуры центра от
F
0
при
мгновенном изменении температуры
поверхности
Температура по толщине тела распределяется по закону косинуса, закону
параболы, поэтому значение температуры в любой точке тела, находящейся на
расстоянии
x
от центра пластины или от оси цилиндра, можно определить
по формулам:
;) / )(
(
2
Sx t t
t t
ц
п
ц
− + =
(6.83)
.) / )(
(
2
Rr t t
t t
ц
п
ц
− + =
(6.84)
Если в начальное условие ввести уравнение (6.83) или (6.84) при граничных
условиях первого рода
t
п
= const, то этот случай приобретает большое
практическое значение. Он соответствует случаю нагрева слитка или заготовки
после того, как температура их поверхности достигла заданной величины и
остаётся постоянной, а температура центра приближается к температуре
поверхности (так называемая выдержка).
Решение задачи для этого случая можно выразить бесконечным рядом
аналогично формуле (6.80) или формулой
(
) (
)
θ
′ = −
− = ′
цн
п
ц
п
F
.
0
) (
t t t t
f
,
(6.85)
где
t
н.ц
– начальная температура центра слитка или заготовки. Значения
f
'(F
0
)
для пластины и цилиндра в зависимости от F
0
могут быть взяты из
графика на рис. 6.28.
Если отбросить все члены бесконечного ряда, кроме первого, что возможно
для пластины при F
0
= 0,06 и цилиндра при F
0
= 0,08, то получим для пластины
(
) (
)
)
47,2 exp(
03,1
0
.
F
t t t t
⋅
−
= −
−
цн
п
ц
п
;
(6.86)
Цилиндра


