ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
134
(
) (
)
)
76,5 exp(
11,1
0
.
F
t t t t
⋅
−
= −
−
цн
п
ц
п
(6.87)
Величину теплового потока на поверхности тела можно найти по формулам
для пластины
( )
(
)
( )
0
.
1
2
Ff t t S
q
′′
−
=
−
цн
п
п
λ
(6.88)
Цилиндра
( )
(
)
( )
0
.
1
2
Ff t t R q
′′
−
=
−
цн
п
п
λ
(6.89)
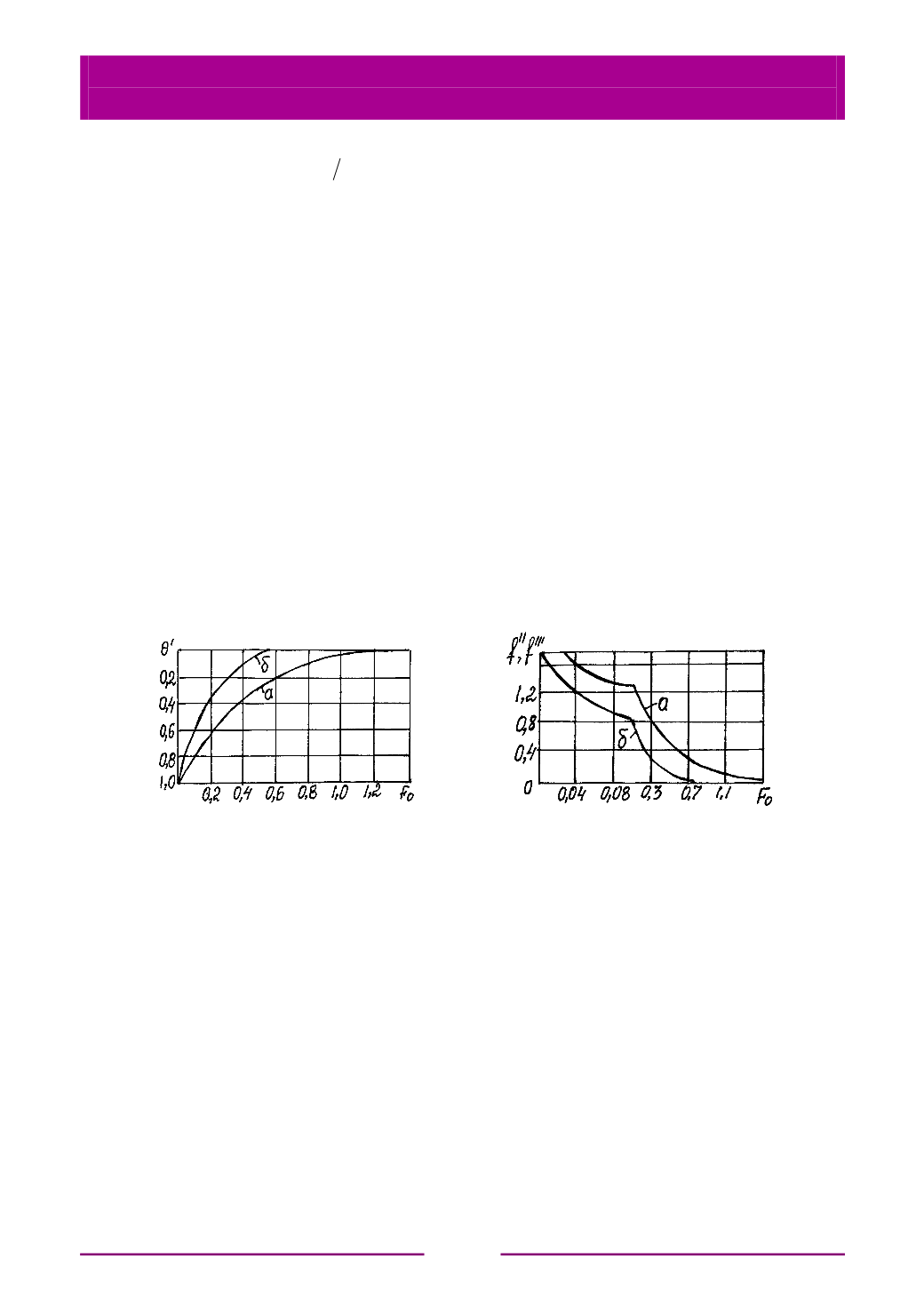
Значения
f
''(F
0
) и
f
'''(F
0
) могут быть взяты из графика на рис. 6.29.
При граничных условиях второго рода задается изменение по времени
теплового потока, проходящего через поверхность тела
q
=
f
(
τ
). В частном
случае
q
= const. Применение граничных условий второго рода ограничено,
например, печами с переменной температурой рабочего пространства.
В частности, к таким печам можно отнести нагревательные колодцы.
Рассмотрим задачу при начальных
t
=
t
н
= const (
τ
= 0) и
граничных –
λ
dt
/
dx
(при
x
=
±
S
) =
q
п
= const условиях.
Рис. 6.28. Кривые выравнивания
температур
t
= const:
а
– для пластины толщиной 2
S
;
б
– для цилиндра радиусом
R.
Рис. 6.29. Функции
f
'' и
f
''' для
определения величины теплового
потока на поверхности тела
:
а
– пластина толщиной 2;
б
– цилиндр радиусом
R
Температуру в любой точке по сечению пластины в этом случае определяем
по формуле
); / , (
)(
0
1
Sx f
Sq t
F
п
−
=
λ
(6.90)
по сечению цилиндра – по формуле
),
/ , (
)(
0
1
Rr f
Rq t
F
п
′
=
−
λ
(6.91)


