ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
137
а
б
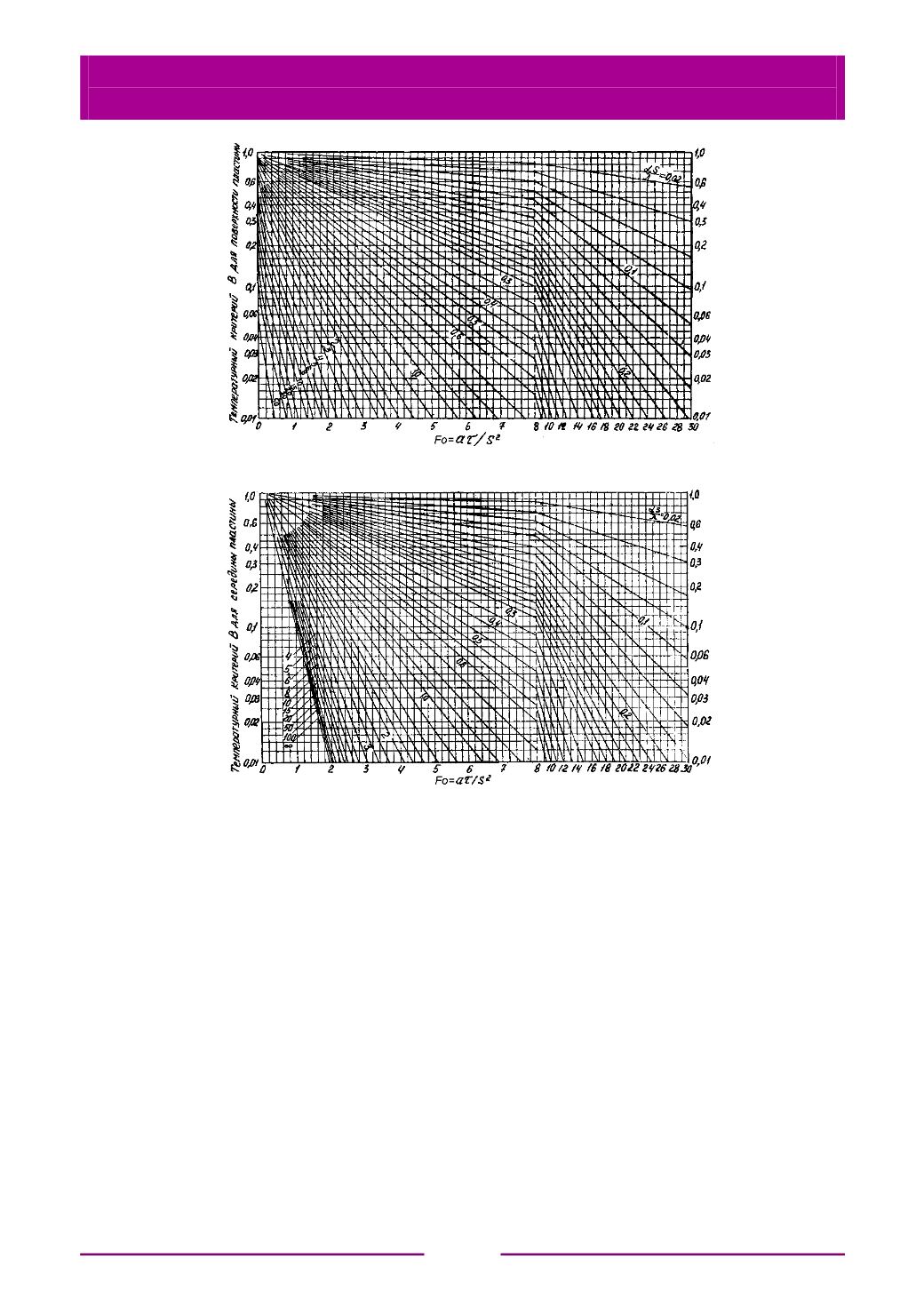
Рис. 6.32. Номограмма для расчета нагрева или охлаждения
поверхности (
а
) и середины пластины (
б
)
Дифференциальное уравнение теплопроводности заменяется на сетке
разностной схемой или уравнением в конечных разностях. После того как и
краевые условия заменены разностными схемами, получаем систему
алгебраических уравнений в конечных разностях с числом неизвестных
(температур), равным числу узлов сетки (уравнений). Важнейшие свойства
разностных схем – аппроксимируемость, устойчивость и сходимость.
Аппроксимируемость схемы означает, что при стремлении к нулю шагов
аргументов решение системы алгебраических уравнений стремится к решению
исходного дифференциального уравнения при заданных краевых условиях.
Устойчивой называют такую схему, для которой ошибки округления,
неизбежные при всяком счете, при уменьшении шагов аргументов
(сгущении сетки) не приводят к большим искажениям решения. В противном
случае схема называется неустойчивой.
а)


