ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
135
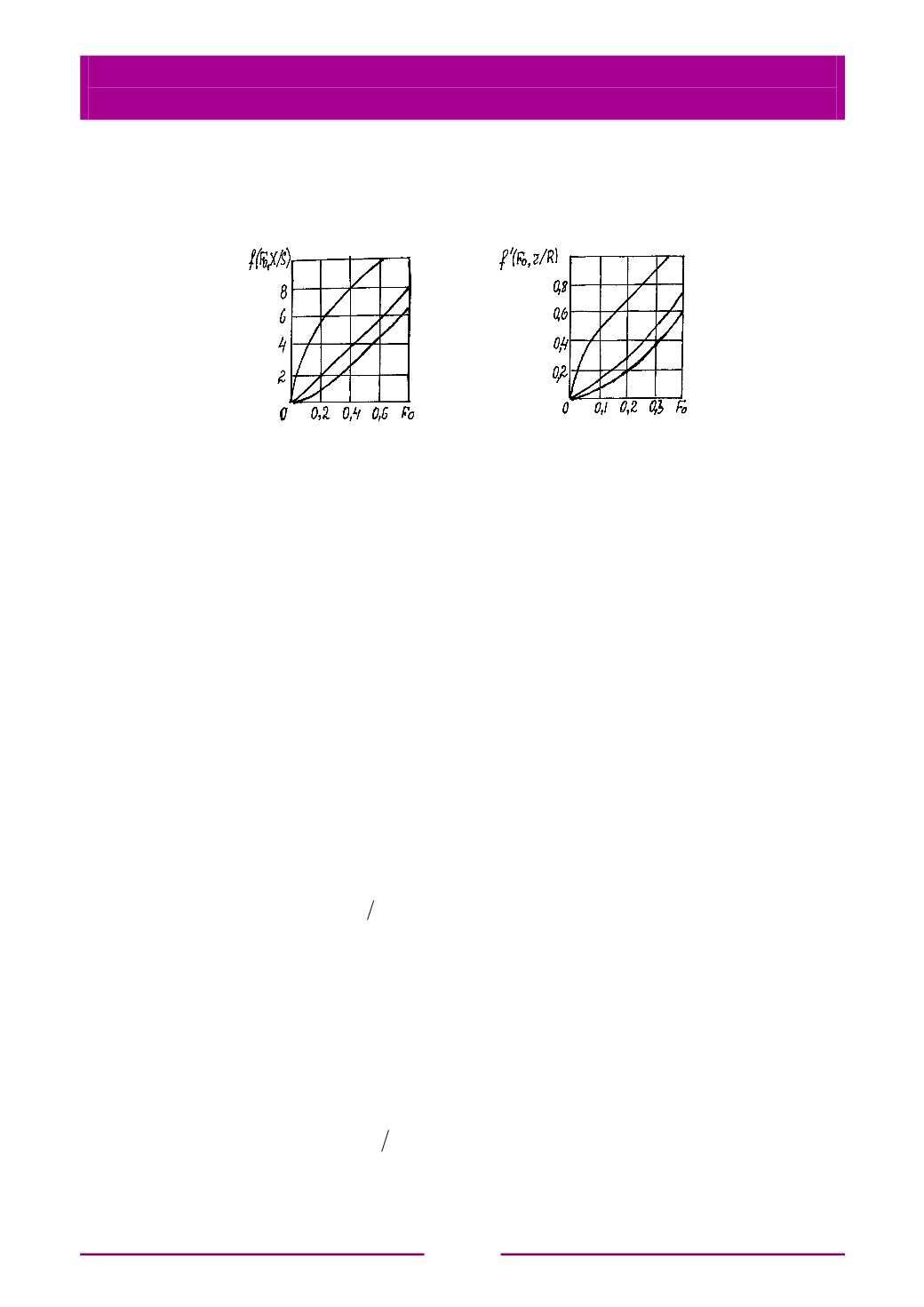
Графики для определения функций
f
(F
о
;
x
/
S
) и
f
'(F
о
;
r
/
R
) в зависимости от
критерия Фурье для поверхности
x
/
S
=
r
/
R
= 1, центра
x
/
S
=
r
/
R
= 0 и для
половины расстояния от центра до поверхности приведены на рис. 6.30.
а
б
Рис. 6.30. Графики для определения функций (F
0
,
х
/
S
) для пластины (
а
)
и (F
0
,
r
/
R
) для цилиндра (
б
) при расчете их нагрева с постоянным
тепловым потоком на поверхности
При граничных условиях третьего рода задаются температурный режим
печи и закон теплообмена между окружающей средой и поверхностью тела,
воспринимающей тепло. Если температура печи постоянна при
τ
= 0,
t
=
t
н.п
= const (начальные условия) и тепло передается по закону
q
п
= -
λ
dt
/
dx
(при
x
=
±
S
) =
α
л+к
(
t
н.п
–
t
п
) (граничные условия), то решение
уравнения теплопроводности (6.6) при граничных условиях третьего рода
находит широкое распространение при расчете печей камерного типа.
Для печей с переменной температурой по длине и методических печей при
усреднении температуры также вполне можно применить условия третьего
рода. Ниже приводится расчет печи с методическим нагревом.
Окончательное
решение
дифференциального
уравнения
(6.6)
в критериальной форме может быть представлено следующим образом:
(
) (
) (
)
Sx
t
t t
t
/ ,
,
0
.
.
FBi
н
пн
пн
= −
− =
θ
(6.91)
где
t
н.п
,
t
н
,
t
– начальные температуры печи и заготовки, переменная
температура нагреваемого тела,
0
С; Bi =
α
S
/
λ
– число подобия Био;
F
0
=
а
τ
/
S
2
– число подобия Фурье;
x
/
S
= безразмерная толщина тела;
S
– расчетная прогреваемая толщина тела, м;
α
– коэффициент теплоотдачи от
печи к телу, Вт/(м
2
⋅
К);
τ
– время нагрева, с.
Для центра нагреваемого тела
x
= 0 и
x
/
S
= 0. Для поверхности
тела
x
=
S
и
x
/
S
= 1. Критериальное уравнение для центра тела
(
) (
)
(
)
0
.
.
.
.
,
FBi
ц
цн
пн
цк
пн
f
t
t
t
t
= −
− =
θ
;
(6.92)
Критериальное уравнение для поверхности тела


