231
Далее представим его в виде внешней функции и применим функцию
y
=
ode
(
x
0,
t
0,
t
,
f
), в качестве параметров которой будем использовать:
f
– ссылка на предварительно созданную функцию
f
(
t
,
x
);
t
– координаты сетки;
x
0,
t
0 – начальное условие
x
(0)=1.5;
y
– результат работы функции.
-->function yd=f(t,x),yd=-x+sin(t*x),endfunction;
-->x0=1.5;t0=0;t=0:1:35;
-->y=ode(x0,t0,t,f);
-->plot(t,y);
-->xgrid();
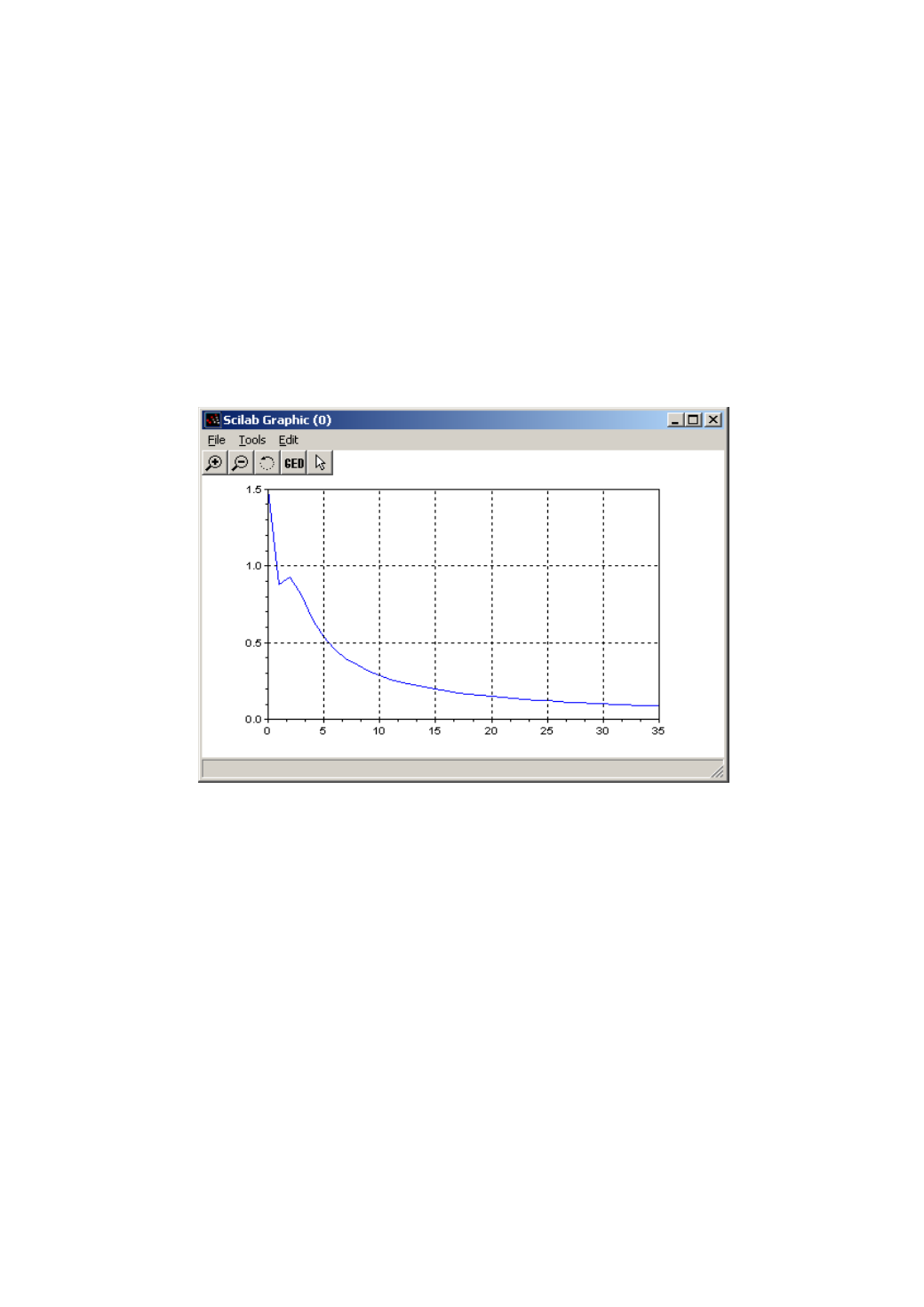
График, моделирующий процесс, описанный заданным уравнением,
представлен на рис. 25.1.
Рис. 25.1. Решение дифференциального уравнения
Пример 25.2.
Решить задачу Коши
( )
(
)
( )
( )
,
,
0 0,
0 0
x cos xy
y sin x ty
x
y
′ =
′ = +
=
=
на интервале [0; 10].
Ниже
приведена
функция,
описывающая
заданную
систему
обыкновенных дифференциальных уравнений и команды Sciab необходимые
для ее численного и графического решения (рис. 25.2).
-->//Функция, описывающая систему дифференциальных уравнений
-->function dy=syst(t,y)
-->dy=zeros(2,1);
-->dy(1)=cos(y(1)*y(2));
-->dy(2)=sin(y(1)+y(2)*t);
-->endfunction
-->//Решение системы дифференциальных уравнений
-->x0=[0;0];t0=0;t=0:1:10;


