53
представлены на рис.2, а. Стоит отметить, что изменение
напряжения практически пропорционально изменению
нагрузки, т.е. чем больше изменение нагрузки, тем больше
изменение
напряжения.
Видно,
что
наиболее
чувствительными к изменению модуля напряжения
являются узлы под номерами 19, 22, 21, 18, 20.
Определим сенсорные узлы по модулю напряжения,
используя сингулярный анализ матрицы Якоби. На
рис. 2, б представлены рассчитанные компоненты первого
правого сингулярного вектора, соответствующие модулям
напряжений в узлах. Сенсорными по модулю напряжения
в узле являются узлы 20, 18, 21,22.
Выполним расчет режима методом голоморфного
погружения и проведем анализ степенных рядов и их
аппроксимантов Паде. На рис. 3 представлены графики
аппроксимантов Паде степенных функций напряжений от
параметра α. Видно, что наиболее сильно напряжение
снижается в узлах 19, 22, 21, 20, 18.
Выполним расчет обратных величин радиусов
сходимостей степенных рядов (рис.2, в), а также нулей и
полюсов аппроксимаций Паде (рис.2, г). Видно, что
профиль гистограмм обратной величины радиуса
сходимости и обратной величины минимального полюса
(нуля) аппроксиманта Паде совпадает. Узлы с
наименьшими радиусами сходимости / полюсами (нулями)
можно считать слабыми. Наиболее слабые узлы 19, 21, 22,
18. Преимуществом способа на основе анализа радиусов
сходимостей является значительное снижение объема
вычислительных операций, в отличие от классических
способов, основанных на вычислительно затратном
анализе матрицы Якоби.
V.
З
АКЛЮЧЕНИЕ
На основе выполненных расчетов можно сделать
вывод, что на основании значений радиусов сходимости
степенных рядов голоморфных функций напряжений и
полюсов (нулей) их аппроксимантов Паде можно выявить
сенсорные узлы по напряжению. Тестовые расчеты
показали, что наиболее сенсорные узла, определенные
предлагаемым методом совпали с определенными с
помощью
классического
утяжеления
режима
и
сингулярного разложения матрицы Якоби.
Стоит отметить, что для более чёткого ранжирования
узлов по степени чувствительности в получившейся
выборке, необходимо использовать методы кластерного
анализа, например, метод
k
-средних или метод
иерархической агломеративной кластеризации.
Список литературы
[1]
Правила
технологического
функционирования
электроэнергетических систем (утв. приказом Минэнерго России от
03.08.2018 № 630).
[2]
Требования к обеспечению надежности электроэнергетических
систем, надежности и безопасности объектов электроэнергетики и
энергопринимающих установок «Методические указания по
устойчивости энергосистем» (утв. постановлением Правительства
Российской Федерации от 13.08.2018 № 937).
[3]
Войтов О. Н., Воропай Н. И., Гамм A. З., Голуб И. И., Ефимов Д. Н.
Анализ
неоднородностей
электроэнергетических
систем.
Новосибирск: Наука. Сибирская издательская фирма РАН. 1999. –
236 с.
[4]
Гамм А.З., Голуб И.И. Обнаружение слабых мест в
электроэнергетической системе// Известия РАН. Энергетика, 1993,
№3. – С. 83–92.
[5]
Белов Е. И., Латманизова Ю. Н., Сорокин Е. В. Применение сингу-
лярного анализа для определения сенсорных по току ветвей в
электроэнерге-тических системах // Электроэнергия. Передача и
распределение, 2018, № 4 (49). – С. 48–52.
[6]
Trias A. The holomorphic embedding load flow method // 2012 IEEE
Power and Energy Society General Meeting. – 2012. – P. 1–8.
[7]
Trias A. Fundamentals of the Holomorphic Embedding Load-Flow
Method,
2015
[Электронный
ресурс].
–
URL:
.
[8]
Rao S., Feng Y., Tylavsky D.J., and Subramanian M.K. The holomorphic
embedding method applied to the power-flow problem // IEEE
Transactions on Power Systems. – 2016. – V. 31. – №. 5. – P. 3816–3828.
[9]
Исаев Ю.Н., Кабалин Д.А. Голоморфное погружение как
аналитический метод расчета электрических сетей нефтяных и
газовых месторождений // Известия Томского политехнического
университета. Инжиниринг георесурсов. – 2020. – Т. 331. – № 4. – С.
115–125.
[10]
Исаев Ю.Н., Кабалин Д.А.. Голоморфное погружение как метод
расчета установившихся режимов электрических сетей нефтяных и
газовых месторождений и оценки их устойчивости // Известия
Томского
политехнического
университета.
Инжиниринг
георесурсов. – 2021. – Т. 332. – № 2. – С. 214–228.
[11]
Бейкер Дж. мл., Грейвс-Моррис П. Аппроксимация Паде. – М.: Мир,
1986. – 502 с.
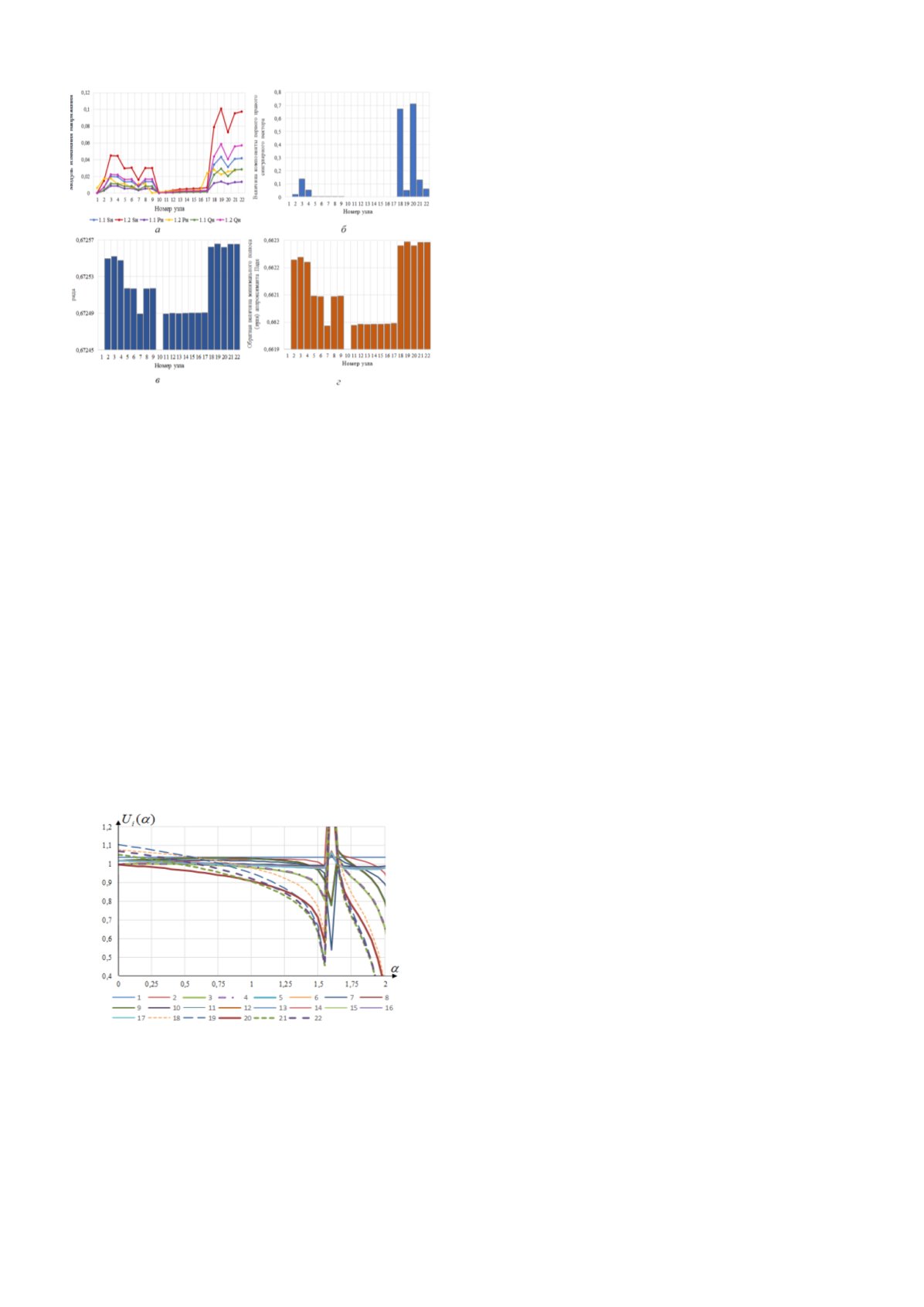
Рис. 2 – Определение сенсорности узлов по напряжению:
а – модуль изменения напряжения (в о.е.) в узле при увеличении
нагрузки, б – величина компонент первого правого сингулярного
вектора, в – обратная величина радиуса сходимости степенного
ряда, г – обратная величина минимального полюса (нуля)
аппроксиманта Паде
Рис. 3 – Графики аппроксимантов Паде степенных функций
напряжений узлов от параметра α


