52
Степень влияния активных и реактивных нагрузок в
узле
j
на изменение фаз и модулей напряжения в узле
i
характеризуют элементы обратной матрицы Якоби
(
)
1
,
,
,
.
−
i
j
i
j
i
j
i
j
J
P Q U P U Q
Графическая
визуализация элементов блок-подматриц
i
j
U Q
и
i
j
U P
, с помощью тепловой карты матрицы или
гистограмм её элементов, позволяет оценить сенсорные
узлы по напряжению. Недостаток метода в том, что
результат является субъективным, т.к. нет четкого
критерия, по которому узлы однозначно следует отнести к
сенсорным, и решение основывается на мнении
исследующего [5].
Сингулярное разложение матрицы Якоби
,
=
T
J W V
где
1
(
)
, ...,
=
k
W
w w
и
1
(
)
, ...,
=
k
V
v v
– ортогональные
матрицы размером
k k
,
i
-е столбцы которых являются
соответственно
i
-м левым и
i
-м правым сингулярными
векторами;
1
(
)
, ...,
=
k
diag
– диагональная матрица
сингулярных чисел [3-5]. Сенсорными узлами являются
узлы с соответствующими максимальными компонентами
первого правого сингулярного вектора. Недостаток метода:
вычисление собственных значений и собственных
векторов матрицы Якоби вычислительно затратно
(большой объем вычислительных операций и, как
следствие, времени). Данный метод не нашел широкого
применения в практических расчетах.
Также сенсорные узлы можно найти, используя метод
продолжения по параметру (метод прогрессивного
потокораспределения, continuation power flow, CPF),
применяемый для определения точки коллапса напряжения
(точки бифуркации) при увеличении нагрузки в
энергосистеме.
III.
П
ОИСК СЕНСОРНЫХ УЗЛОВ НА ОСНОВЕ АНАЛИЗА
ГОЛОМОРФНЫХ ФУНКЦИЙ НАПРЯЖЕНИЙ
Метод голоморфного погружения (holomorphic
embedding load flow method, HELM) основан на
комплексном
анализе
и
теории
аналитического
продолжения [6-10]. Преимуществом метода является то,
что для него не нужно задавать начальное приближение,
как в классических итерационных методах расчета УР.
При расчете УР методом голоморфного погружения
неизвестные напряжения узлов представляются в виде
голоморфных функций, которые можно представить в виде
степенного ряда Тейлора:
2
( )
[0]
[1]
[2]
...
[ ] ,
,
= +
+
+ +
+
n
i
i
i
i
i
U U U U
U n i PQ PV
(2)
где
[ ]
i
U n
–
n
-ый коэффициент степенного ряда функции
напряжения
i
-ого узла, определяемый путем решения
рекуррентного матричного уравнения [11];
α –
параметр
погружения.
В целях улучшения точности решения для каждого
степенного ряда находится диагональная (
L
=
M
) или
близкодиаганальная (
L
=
M –
1) аппроксимация Паде [12]:
0
( )
0
0
[ ]
(
)
(
)
[ ]
/
,
( )
[ ]
+
=
=
=
=
=
= =
L
n
L M
n
n
M
f
n
n
n
a n
a
f
c n
L M
b
b n
(3)
В работе [11] для оценки приближения решения
системы УР к границе устойчивости предлагалось
применять нули и полюса аппроксимации Паде,
расположенные вдоль действительной оси комплексной
плоскости. Самый левый полюс (нуль) по действительной
оси определяет точку ветвления, которая характеризует
предельное значение коэффициента
,
на которое
пропорционально
можно
увеличить
нагрузку
и
нерегулируемую
генерацию,
чтобы
решение
существовало.
Величина обратная минимальному полюсу (нулю)
(точке ветвления) аппроксиманта Паде характеризует
степень сенсорности узла по напряжению. Точка ветвления
без расчета полюсов и нулей аппроксимации Паде может
быть приближенно определена через радиус сходимости
степенного ряда:
[ ]
lim
,
[ 1]
→
=
+
i
i
n
i
U n
R
U n
(4)
Обратная величина радиуса сходимости (1/
R
i
) также
может быть использована для выявления слабых узлов.
IV.
Т
ЕСТИРОВАНИЕ МЕТОДА
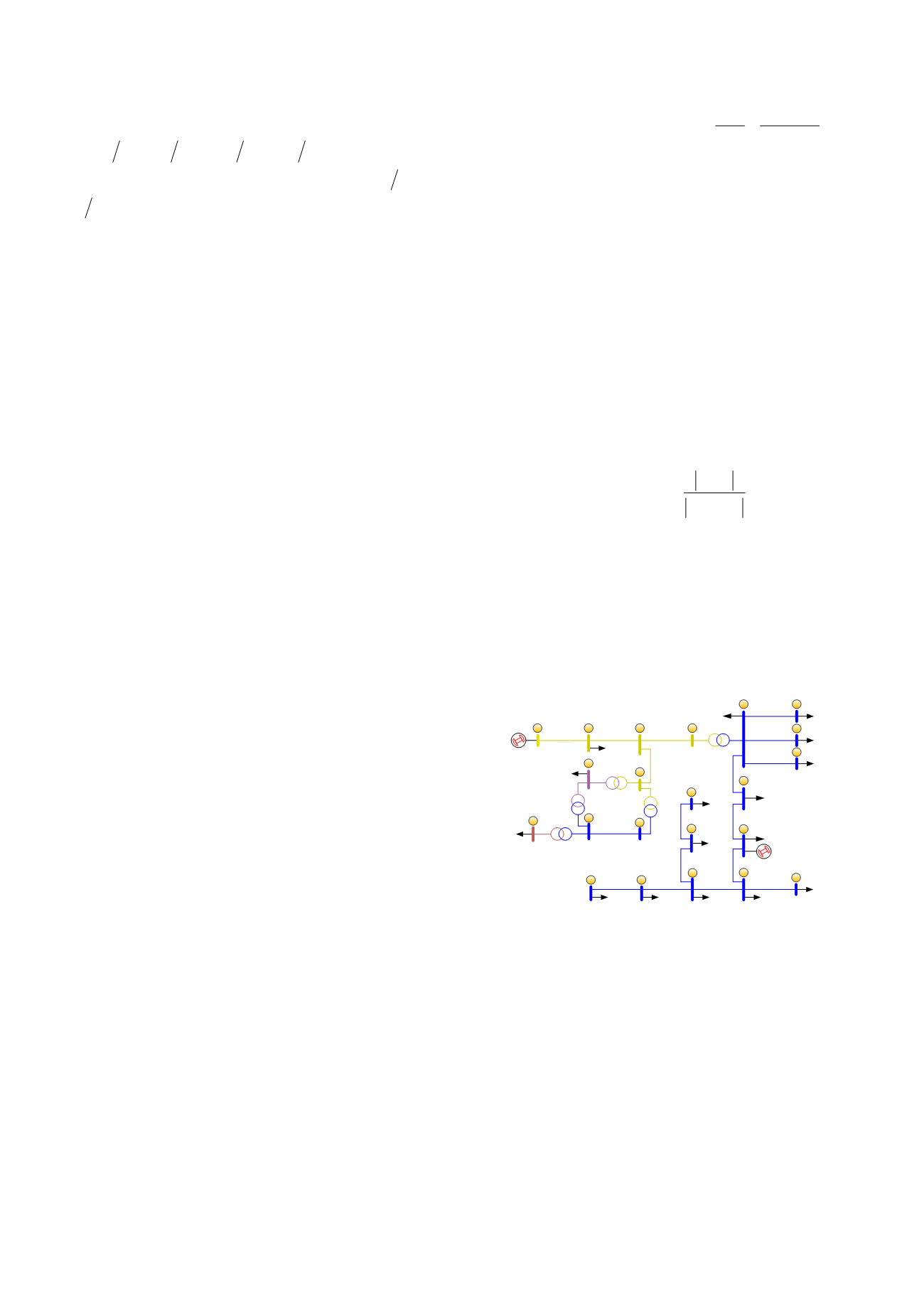
Для тестирования метода использовалась 22-узловая
тестовая схема, представленная на рис. 1.
Произведем анализ в ПК
RastrWin3
. Для этого
используем различные способы утяжеления режима:
одновременное увеличение активной и реактивной
мощностей нагрузки во всех узлах на 10 % и 20 %,
увеличение активной мощности нагрузки в каждом узле на
10 % и 20 %, увеличение реактивной мощности нагрузки в
каждом узле на 10 % и 20 %. Результаты расчетов
Рис. 1 – Тестовая схема электрической сети
|U
Б
|
=1,0348
0,0175+j0,0633
0,1412
1
2
3
4
5
6
8
9
7
10
11
12
13
14
15
16
17
19
20
22
0,0431+j0,1554
0,3497
0,0173+j0,0508
0,1095
0,003+j0,17
0,0031+j0,354
0,2722+j0,2571
0,0284
0,1119+j0,3327
0,0442
0,2707+j0,2253
0,0247
0,1021+j0,096
0,0106
0,1104+j0,313
0,0413
0,0572+j0,0862
0,0104
0,1868+j0,1769
0,0194
0,09+j0,1353
0,0161
0,0715+j0,1081
0,013
0,1127+j0,1406
0,0164
0,085+j0,08
0,009
0,1444+j0,1815
0,0211
18
0,0057+j0,2155
0,0028+j0,0002
0,926
0,0264+j0,3759
0,9381
0,0064+j0,1418
0,9381
0,0059+j0,0008
0,9814
0,9804
0,1+j0,06
P
10
=0,05
|U
10
|
=1,0
0,018+j0,01
0,007+j0,005
0,027+j0,017
0,004+j0,002
0,105+j0,06
0,105+j0,06
0,01+j0,006
0,023+j0,013
0,008+j0,005
0,02+j0,01
0,005+j0,003
0,015+j0,01
0,016+j0,011
0,31+j0,12
0,02+j0,211
БУ
21


