56
Однако, модуль падения напряжения также можно
рассчитать по второму закону Кирхгофа, согласно рис.2:
(
)
( )
( )
Σ
=
−
d
УУПК
N I I x X I
()
С помощью математических преобразований получено
уравнение:
(
)
(
)
6
1
2
10
( )
d
УУПК
УУПК
N I
I x
I
ω K K I
=
−
−
Σ
()
III.
В
ЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
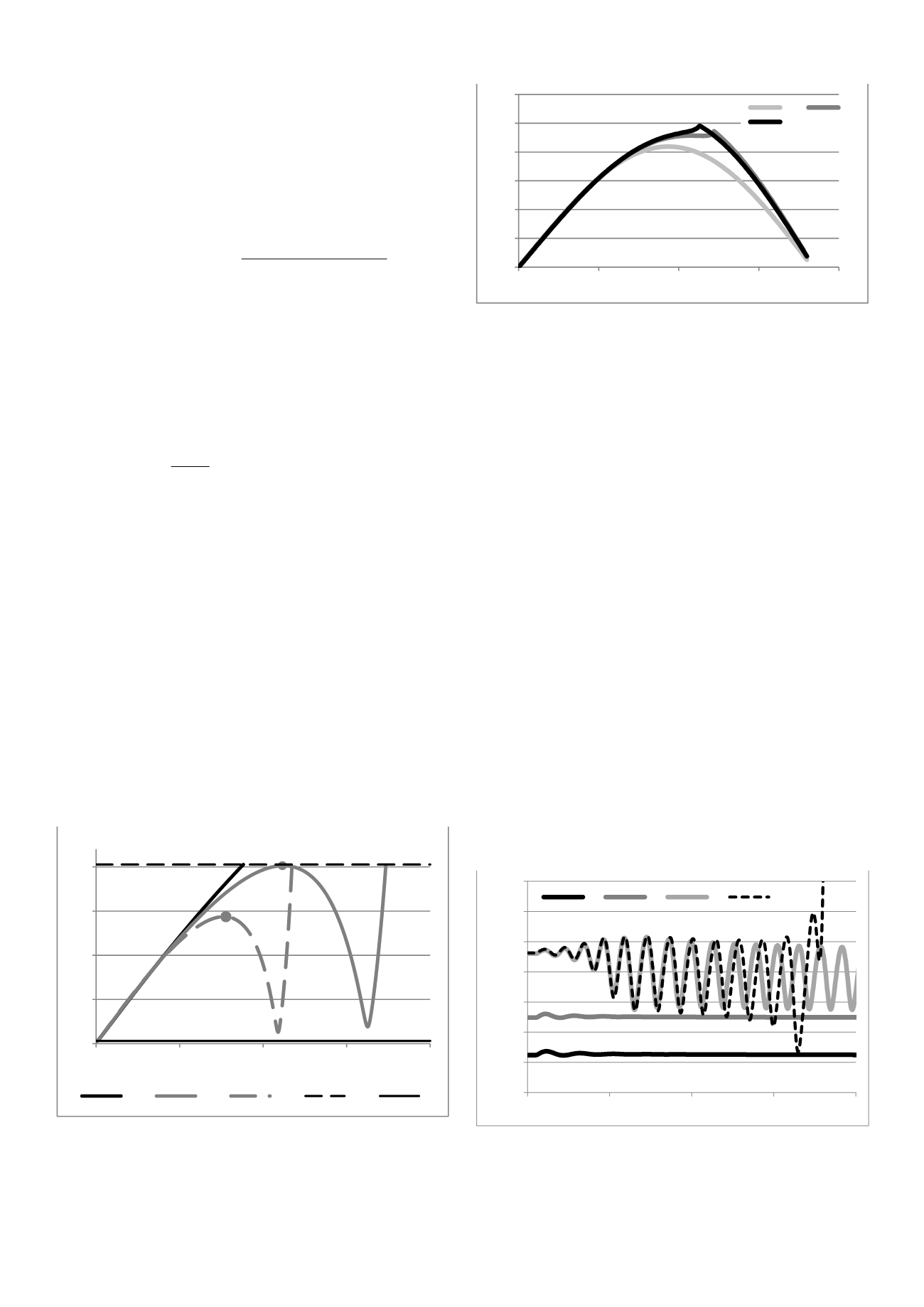
На рис. 5 представлены зависимости модуля
напряжения от тока через УУПК для различных законов
регулирования. Из результатов построения можно сделать
вывод о том, что увеличение коэффициента регулирования
К
2УУПК
приводит к тому, что значение |
N
(
I
)| не доходя до
значения
N
max
начинает снижаться. Данное явление
приводит к тому, что в диапазоне от
N
min
до
N
max
имеется
точка, в которой
( )
0
N I
I
=
(рис.5, а), которая соответствует
началу резонансного перехода. Происходит данное
явление из-за быстрого роста вычитаемого в (4). Таким
образом, резонансный переход приведет к резкому
изменению электромагнитной мощности генераторов и
потере устойчивости системы [4].
Следовательно, чтобы избежать резонансного перехода
и его последствий при этом получив максимальный эффект
от управляемой продольной компенсации выбран такой
закон регулирования, при котором в момент начала
резонансного
перехода
(рис. 5,
а)
коэффициент
регулирования
K
2УУПК
=0
. Таким образом, угловая
характеристика
после
ограничения
становится
традиционной, как для системы с неуправляемой
продольной компенсацией, и показывает увеличение
предельной по статической устойчивости активной
мощности.
На
рис.
6
представлены
угловые
характеристики
при
ограниченно-зависимой
характеристике
X
УУПК
для
различных
законов
регулирования УПК.
Рис. 5 – Зависимость модуля падения напряжения на
электропередаче от тока через УУПК для различных законов
регулирования УПК: 1 – K
2УУПК
= 10; 2 – K
2УУПК
=18; 3 – K
2УУПК
=31;
4 – максимальное падение напряжения на электропередаче Nmax;
5 – минимальное падение напряжения на электропередаче Nmin
Рис. 6 – Угловые характеристики при ограниченно-зависимой
характеристики
X
УУПК
(
I)
для различных законов регулирования УУПК:
1-
К
2УУПК
=10; 2-
К
2УУПК
=28; 3-
К
2УУПК
=30
Традиционно
статическая
устойчивость
электроэнергетической системы оценивается по корням
характеристического уравнения или соответствующим
критериям [5]. В случае если характеристическое уравнение
имеет высокий порядок, то отыскание его корней становится
весьма трудоемкой задачей, поэтому обычно для оценки
устойчивости системы используют алгебраические и
частотные критерии, связывающие корни с коэффициентами
характеристического
уравнения.
Современные
вычислительные средства позволяют также анализировать
статическую устойчивость без линеаризации системы
дифференциальных уравнений, описывающих исследуемую
систему, а именно с помощью вычислительного
эксперимента по детальной математической модели при
возникновении «малого» возмущения. По результату
протекания переходного процесса формируется вывод об
устойчивости энергосистемы.
IV.
Р
ЕЗУЛЬТАТЫ
Каждый конкретный режим ЭЭС имеет свою область
устойчивости. При фиксации степени компенсации
производен вычислительный эксперимент по определению
границы статической устойчивости. Мощность турбины
кратковременно (на 0,05 с) повышается на 5% от значения в
исходном установившемся режиме. Результат протекания
переходного процесса рассматривается на изменении угла
ротора
δ
12
. На рис. 7 представлены графики зависимостей
системы с электропередачей, выполненной проводом марки
АС-500/64 для различных законов регулирования УУПК.
Рис. 7 – Зависимости угла положения ротора
δ
12
от времени при
различных коэффициентах
К
2УУПК
для системы с ЛЭП, выполненной
проводом марки АС-500/64
: 1 - К
2УУПК
=0; 2 - К
2УУПК
=10;
3 - К
2УУПК
=21,7; 4 - К
2УУПК
=21,8
а
а
0
0.5
1
1.5
2
0
0.5
1
1.5
2
|N|, о.е.
I, о.е.
1
2
3
4
5
N
max
N
min
0
0.1
0.2
0.3
0.4
0.5
0.6
0
50
100
150
200
P, о.е.
δ, град
1
2
3
53
54
55
56
57
58
59
60
0
2
4
6
8
δ, град
t, с
1
2
3
4


