" Н а у к а м о л о д ы х " , 3 0 - 3 1 м а р т а 2 0 1 7 г . , А р з а м а с
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
500
Таблица 1. Результаты расчетов задачи 1.
Классический метод
Оптимизированный
программный
Определить
расстояние
1 обл. : 71.4 ─ 63.2 = 8.2
2 обл. : 76.5 ─ 63.2 = 13.3
3 обл. : 61.2 ─ 61.2 = 0
4 обл. : 61.2 ─ 61.2 = 0
Для 1, 3, 4 области:
63.16 – 63.16 = 0
Для 2 области:
84.21 – 63.16 = 19.05
Оптимальный
параметр
частот
распределений
Для гетеродина:
[35.7 .. 39.8], ∆ = 4.2
Для сигнала:
[98.0 .. 102.0], ∆ = 4.0
Для гетеродина:
[31.58 .. 42.11], ∆ = 10.53
Для сигнала:
[94.74 .. 105.26], ∆ = 10.52
Вычислить
параметр
Q = Fс / Fг
Fc = 100
Fг = 37.756
Q = 2.648586
Q = 2.714286
Расчет моделирования реальных систем с частотой гетеродина не
равной нулю и определение оптимальных значений частот сигнала и полосы
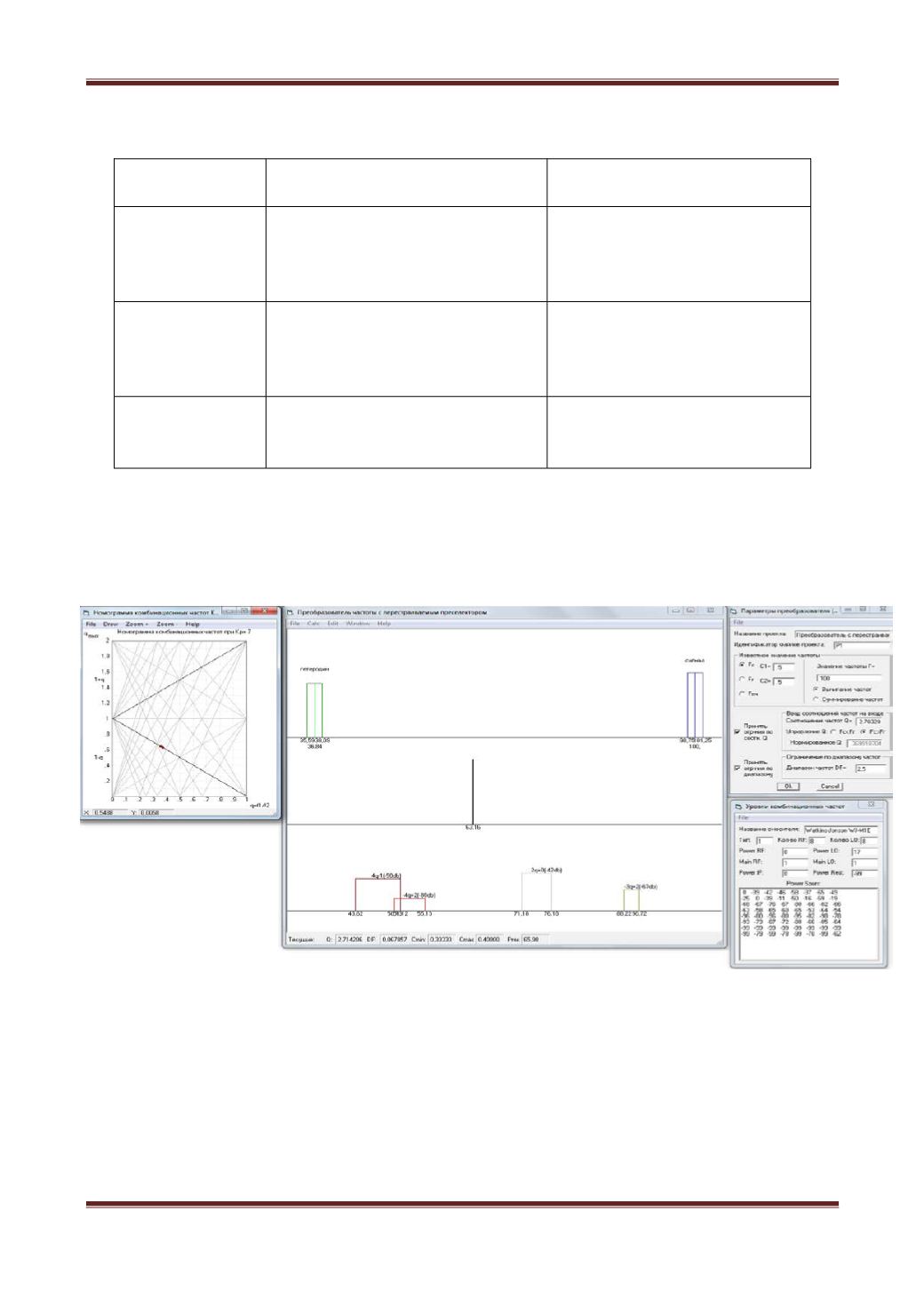
входных частот, см. рисунок 6:
Рис. 6.Результаты расчета реальной системы программы FDMv1 для
задачи 1
∆чд = 8.02 , DF = 2.5
Сравнение результатов компьютерного моделирования идеальной
модели и её расчета классическим методом, представленным в книге


