М а т е р и а л ы X В с е р о с с и й с к о й н а у ч н о - п р а к т и ч е с к о й к о н ф е р е н ц и и
285
Особенность последовательности чисел состоит в том, что каждый её
член, начиная с третьего, равен сумме двух предыдущих. Например, 2 + 3 = 5;
5 + 8 = 13; 8 + 13 = 21 и т.д. Отношение смежных чисел ряда, начиная с пятого,
приближается к отношению золотого деления:
;
Если члены ряда Фибоначчи умножить на одно и то же положительное
число, то полученный ряд будет иметь такие же свойства.
Числа Фибоначчи оказались связанными со многими задачами геометрии
и математического анализа, в частности с задачей о нахождении оптимальной
стратегии поиска приближённого экстремума функции на данном интервале. С
помощью этих чисел была решена одна из важных математических проблем –
десятая проблема Гильберта [2].
Числами
Фибоначчи
описываются
некоторые
количественные
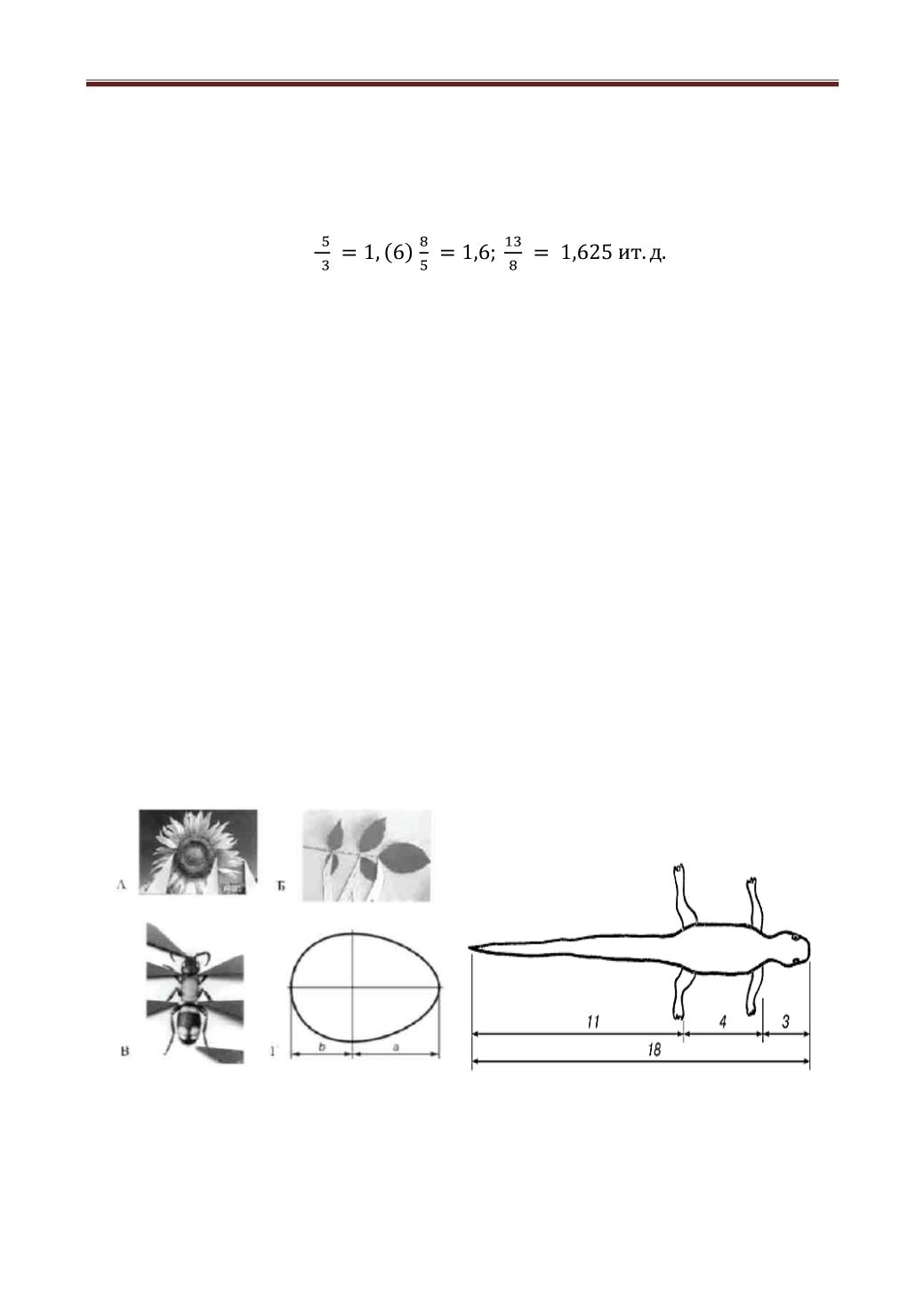
соотношения в растительном мире. Например, семечки в корзинке подсолнуха
расположены по спиралям, закрученным в двух направлениях (рисунок 5, а).
Аналогично расположены цветки в соцветии ромашки, чешуйки на многих
шишках и т.д. При этом количество спиралей разных видов выражается, как
правило, соседними числами Фибоначчи. Например, у ромашки количество
спиралей, идущих в разных направлениях, может равняться 13 и 21, а у
крупных подсолнухов – 55 и 89 [2].
Золотая пропорция широко распространена в растительном и животном
мире. Её можно обнаружить в соотношениях различных частей растений,
насекомых, яйцах птицы (рисунок 5, г). Длина хвоста ящерицы относится к
длине тела как 62 к 38 (рисунок 5, д).
Д
Рис. 5 - Золотая пропорция в живой природе
Биологические исследования показали, что золотое сечение проявляется
всюду, начиная с вирусов и кончая организмом человека. Тело человека линией


