63
4) наблюдение деления ядер нейтронами.
4.8.1. Метод ядер отдачи
Существующие методы регистрации заряженных частиц, в том числе и
ядер отдачи, применимы к частицам не очень малых энергий. Например: ка-
меры Вильсона, пропорциональные счетчики и многие виды фотоэмульсий
удовлетворительно регистрируют тяжелые частицы с энергией не ниже 100
кэВ. Так как энергия ядра отдачи не может быть больше чем энергия ней-
трона, то этот метод применим для регистрации нейтронов средних и боль-
ших энергий.
Ограничиваясь в дальнейшем нерелятивистским случаем упругого рас-
сеяния нейтронов на ядрах, будем в лабораторной системе координат счи-
тать последние покоящемся до их взаимодействия с нейтронами.
При исследовании многих вопросов взаимодействий частиц весьма по-
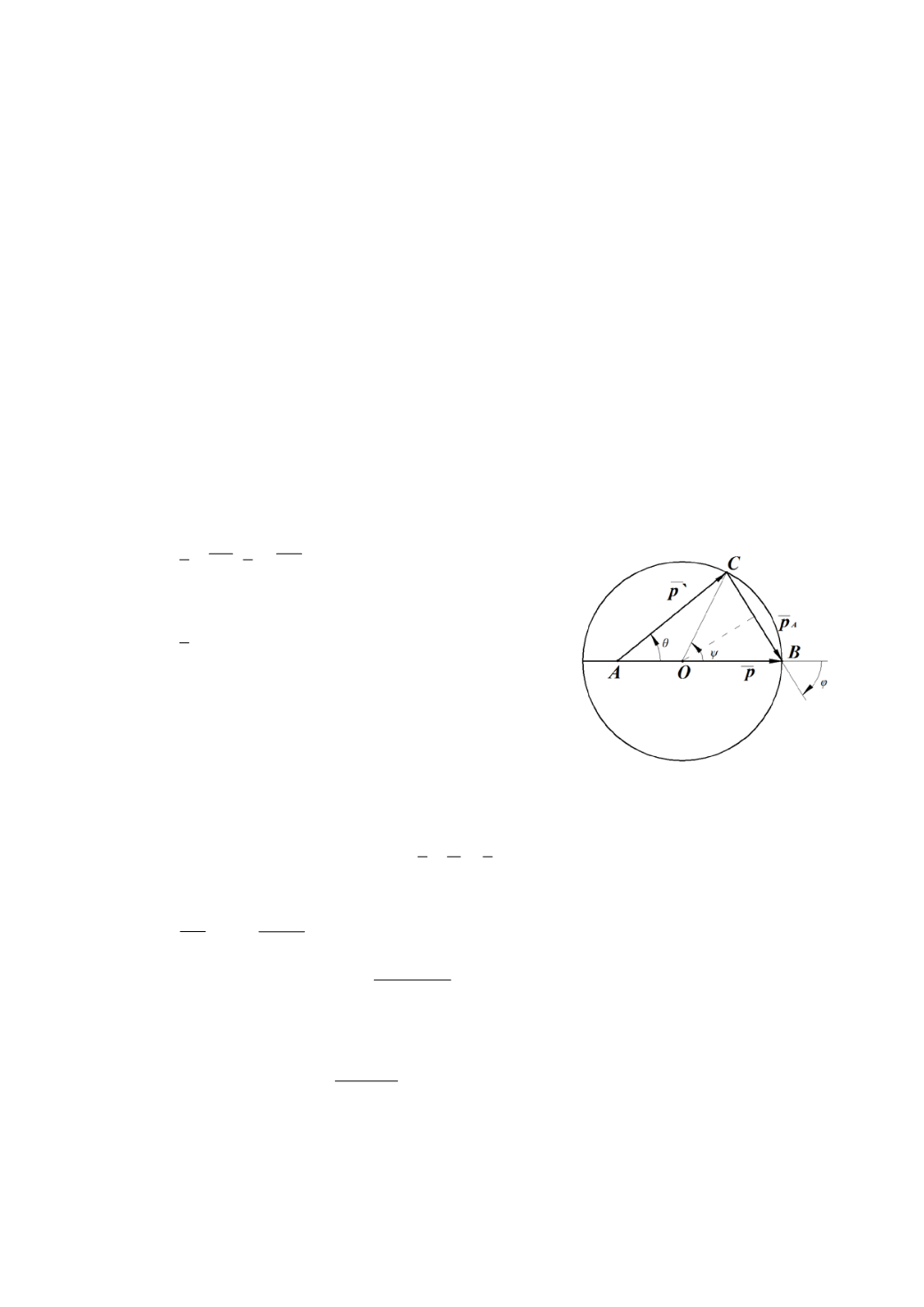
лезной оказывается импульсная диаграмма рассеяния. Такая, диаграмма для
упругого рассеяния нейтрона (масса
m
) на ядре (масса
М >m
) изображена на
рис 45.
На этой диаграмме использованы обозначения:
AC p;AB p
=′
=
- импульсы нейтрона
до и после рассеяния в лабораторной
системе координат (в Л – системе);
A
p
- импульс ядраотдачи (вЛ– системе);
θ и φ - углы рассеяния нейтрона и
ядра отдачи в Л – системе;
ψ - угол рассеяния нейтрона в сис-
теме центра инерции (в Ц – системе).
Используя для упругого рассеяния
нейтрона на ядре законы сохранения энергии и импульса
A n
n
E E E
+′ =
,
A
p p p
+′ =
,
(1)
а также формулы, связывающие энергии частиц с их импульсами
/
m
p E
n
2
2
=
,
M
) p( E
A
A
2
2
=
/, можно найти энергию ядра отдачи
2
2
2
)
cos(
)
cos(
4
)
(E )
(
)mM(
mM E E
n
n
A
ϕ ⋅ α= ϕ ⋅
+
⋅
=
. (2)
Полагая массу нейтрона равной единице, а массу ядра отдачи равно его
массовому числу
А
, для α получаем выражение
2
1
4
) A(
A
+
=α
.
(3)
Из формулы (2) следует, что при рассеянии моноэнергетических ней-
тронов ядра отдачи могут иметь любые энергии в интервале от 0 до α
E
n
.
Максимальное значение энергии, равное α
E
n
, имеют ядра, рассеиваемые на
угол φ=0. В частности, энергия протона отдачи (α=1) при φ=1 равна перво-
Рис. 45


