207
0
(
)
( )
,
(
1)
s
c
верх
c
c
s
r
B H H
B H
H
H H H B B
+
=
+
+ +
−
(7)
0
(
)
(
)
,
(
1)
s
c
низ
c
c
s
r
B H H
B H
H
H H H B B
−
=
+
− +
−
(8)
( )
( )
( )
,
2
верх
нижн
сред
B H B
H
B H
+
=
(9)
где
µ
0
= 4π∙10
-7
−
магнитная проницаемость вакуума,
Гн/м.,
Ввиду малых значений второй составляющей в
выражениях (7) и (8), ими можно пренебречь.
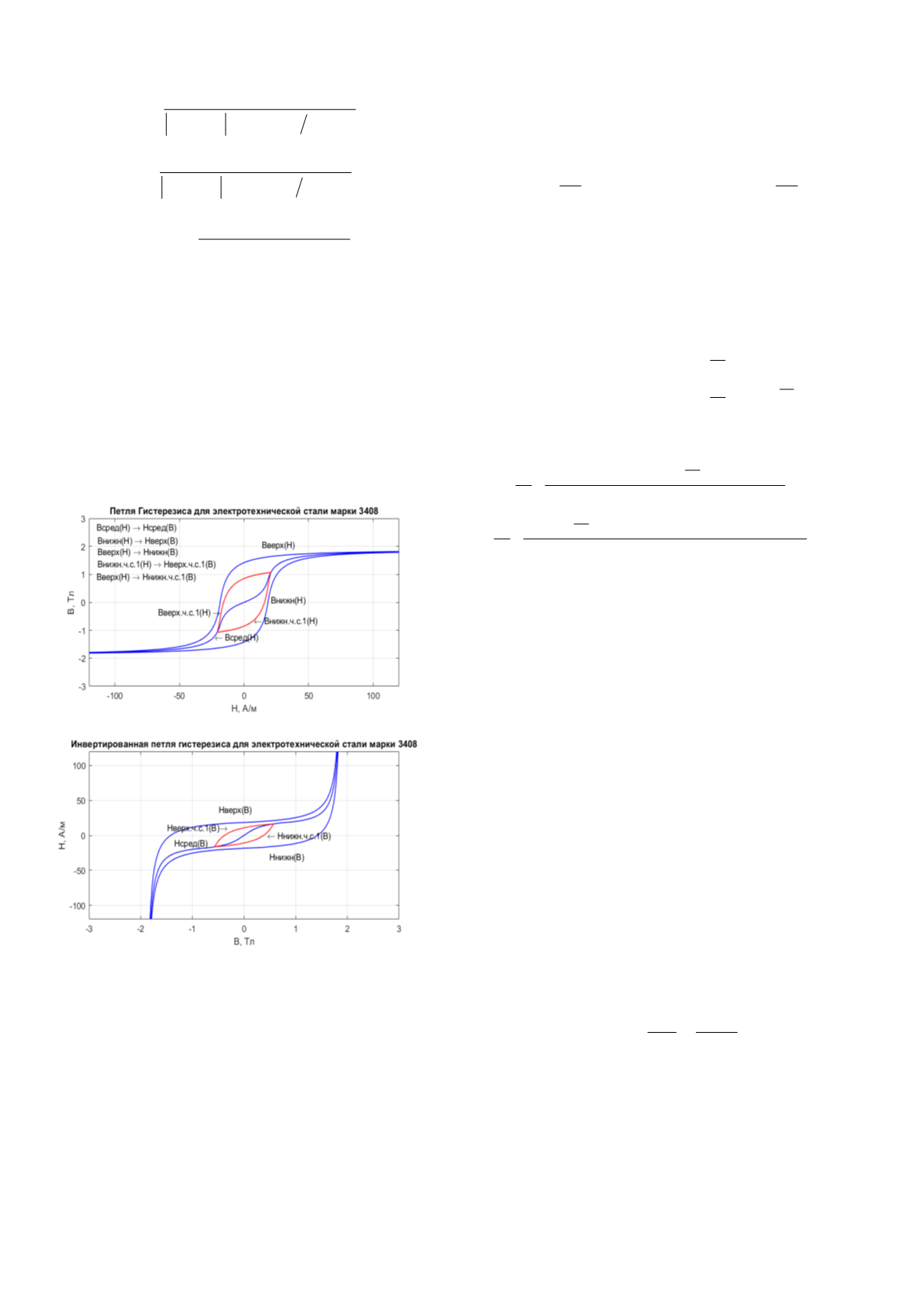
С помощью выражений (7) – (9) была построена
предельная петля гистерезиса и основная кривая
намагничивания для электротехнической стали марки
3408, используемой в ТТ марки ТВТ-110. Для облегчения
дальнейших расчетов и корректной работы модели следует
перейти от представления кривой намагничивания в виде
функции B=f(H) к функции H=f(B), полученные кривые
представлены на Рис.1.
Рис. 1 – Предельная и частная симметричная петля гистерезиса
С помощью методов программной аппроксимации в
MATLAB были получены уравнения, описывающие
кривые H=f(B), в виде полиномов 21 степени. Погрешность
аппроксимации таким методом в соответствии с методом
наименьших квадратов составила 5.7098∙10
-4
.
21
(1)
...
(21)
(22),
H a
B
a B a
=
+ + +
(10)
где
a(N)
−
массив известных коэффициентов
полученных в ходе программной аппроксимации кривых
намагничивания.
Учитывая (10) получим следующую систему для
описания работы ТТ:
21
1 1 2 2
2
2
2
2
2
( (1)
...
(21)
(22))
,
(
) (
)
об
н
об
н
a B
a B a l
i w i w
di
d
w s
i
r r L L
dt
d
B
t
+ + +
= −
=
+ + +
(11)
MATLAB имеет ряд встроенных решателей систем
дифференциальных уравнений, например, решатель
«ode45», основанный на методе Рунге-Кутта 4,5 порядка.
Для его использования следует привести систему (11) к
виду Коши.
Запишем систему в матричной форме:
2
2
2
2
20
1
2
2
1
(
)
(
)
,
( (1) 21
...
(21))
об
н
об
н
d
i r r
w s
L L
dt
di
a
B
a l
w
di
w
dt
dt
B
+
− +
=
+ +
(12)
Тогда в форме Коши:
1
2 2
2
1
2
2
20
2
2
20
1
2
1
2
2
2
2
20
2
2
(
)
(
)
( (1) 21
...
(21)) (
)
,
( (1) 21
...
(21))
(
)
( (1) 21
...
(21)) (
)
об
н
об
н
об
н
об
н
об
н
di
w i r r w L L
d
dt
dt w s a
B
a l L L
di
w s w a
B
a l i r r
di
dt
dt
w s a
B
a
B
l
L L
+ +
+
=
+
+ +
+
−
+ +
+
=
+
+ +
+
(13)
Чаще всего ТТ работает в режимах не соответствующих
предельной петле гистерезиса, а по некоторым частным
кривым характеризующимися меньшими значениями Н.
Авторами данной статьи был написан алгоритм в среде
MATLAB&Simulink,
данный
алгоритм
способен
автоматически строить симметричные частные петли по
значениям B и Н характеризующими режим в конкретный
момент времени в соответствии моделью Джона Чана, а
также строить частные несимметричные петли по
модернизированной модели Джона Чана, частично
описанной в [3]. Частные петли также описываются
полиномиальными уравнениями того же порядка что и
(10), поэтому могут использоваться в вышеописанной
модели ТТ.
Симметричные частные петли получаются путем
смещения вверх нижней кривой или вниз верхней кривой,
когда смещения по B не превышает значения Br. Результат
работы алгоритма для создания симметричных частных
петель показан на Рис.1. Частные несимметричные петли,
когда смещение по B превышает значения Br, создаются
также путем смещения одной из характеристик вверх или
вниз и ее совмещением с расчетной характеристикой,
которая описывается также полиномом исходя из
соотношения длин отрезков AC, AD, A’C’, A’D’,
показанных на Рис.2.:
'
'
,
'
'
AC
A C
AD A D
=
(14)
Далее с помощью программных средств определяются
точки пересечения двух отдельных характеристик и
создается одна общая. Результатом решения (14) также
является полином вида (15), который может быть
использован в системе (13)
21
(1)
...
(21)
(22),
H b
B
b B b
=
+ +
+
(15)


