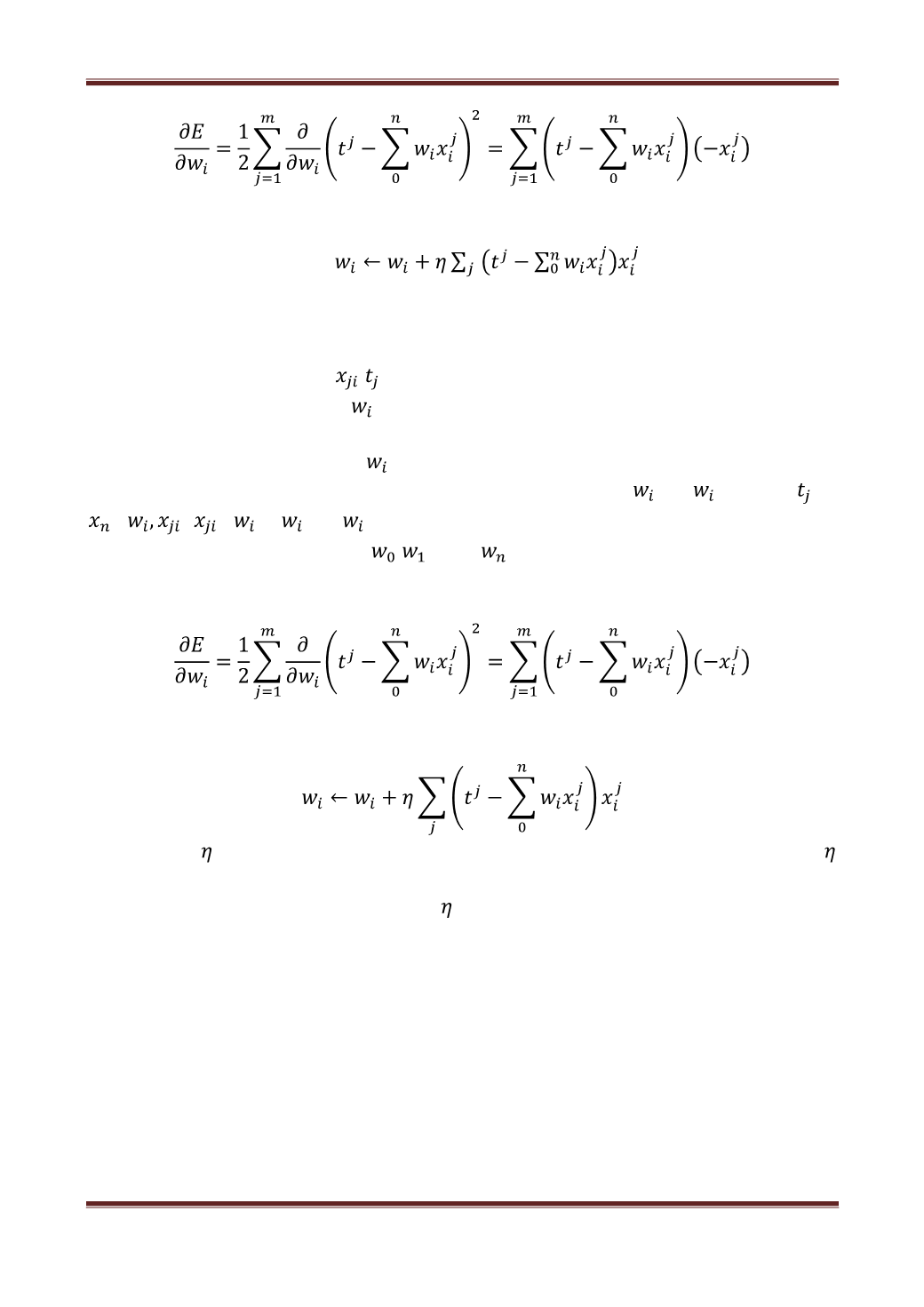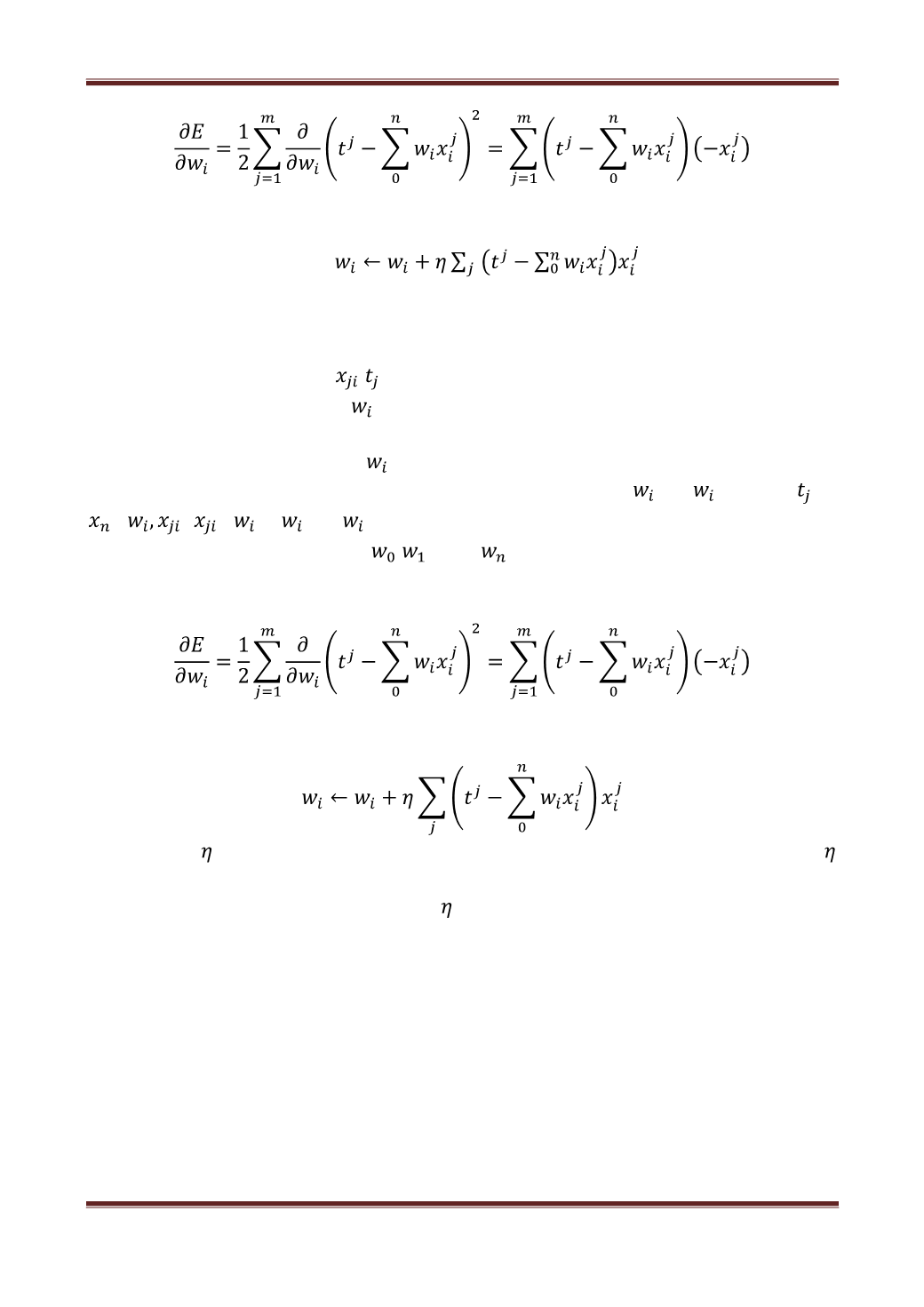
М а т е р и а л ы X В с е р о с с и й с к о й н а у ч н о - п р а к т и ч е с к о й к о н ф е р е н ц и и
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
479
Изменения весов примут вид:
.
Чтобы осуществить это программно, нужно дифференцировать функцию
Е
.
GradientDescent(η, {j , } n,m i=1,j=1 )
1.Инициализировать { }n i=0 маленькими случайными значениями.
2.Повторить NUMBER_OF_STEPS раз:
а) Для всех i от 1 до n ∆ = 0.
б) Для всех j от 1 до m: Для всех i от 1 до n ∆ = ∆ + η t −
0,
! . = + ∆ .
3.Выдать значения , , . . . , .
Выше представлен алгоритм градиентного спуска для одного
перцептрона.
Нужно подправлять веса после каждого тестового примера следующим
образом:
Если будет маленькое – не успеем дойти до минимума, а если
большая, тогда будем перескакивать через него. Для решения это проблемы
нужно начать с достаточно большого , а затем постепенно уменьшать.
Также нужно ввести некоторые изменения. 1) Больше нельзя
рассчитывать на то, что в какой-то момент достигается идеальное соотношение
с исходными данным, и нужно останавливаться в какой-то момент. В качестве
условия для остановки, нужно повторить алгоритм нужное количество раз. 2)
Если оставлять
η
постоянным, то на каком-то этапе вектор весов перестанет
приближаться к искомому минимуму, а начнёт его перепрыгивать на каждой
итерации. Поэтому
η
нужно уменьшать со временем.
В результате работы выделяется область гортани, что позволяет в
дальнейшем определить необходимые для ее исследования характеристики
(рис. 3).