" Н а у к а м о л о д ы х " , 3 0 - 3 1 м а р т а 2 0 1 7 г . , А р з а м а с
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
478
Рис. 2 - Графический пример работы метода
Но учитывая качество некоторых изображений, всегда точно можно
определить границы гортани для дальнейшего анализа.
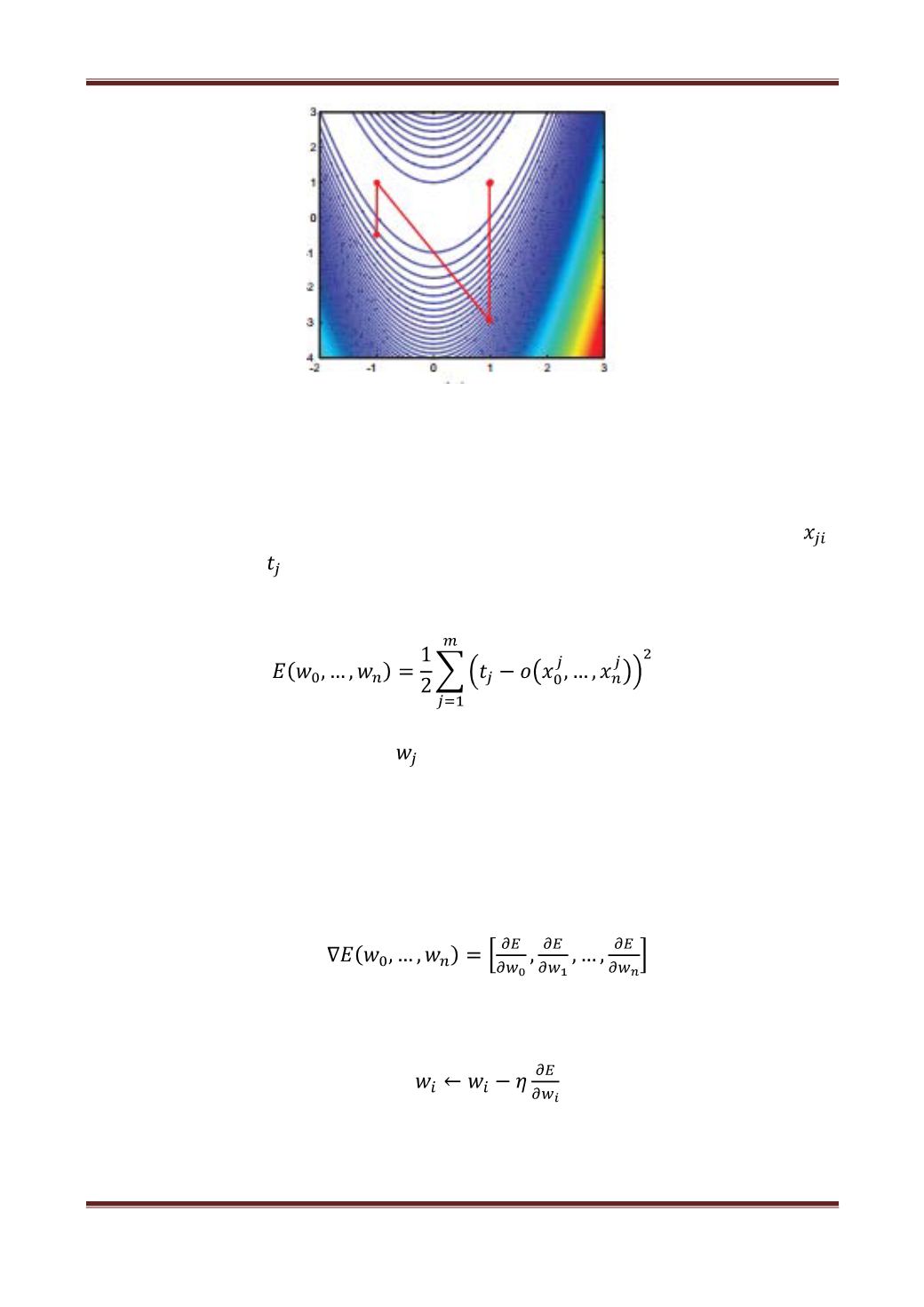
Таким образом, нужно найти перцептрон, который бы в каком-то смысле
минимизировал ошибку. Пусть есть несколько
m
тестовых примеров
с
верными ответами ,
j
=
1..m
.
В качестве границы измерения ошибки возьмём среднеквадратичное
отклонение.
Задача сводится к следующему - минимизировать функцию
E
на
пространстве возможных весов { }.
График
Е
представляет собой параболическую поверхность у которой
должен быть один единственный минимум. Следовательно, нужно исправлять
веса так, чтобы двигаться к этому единственному минимуму. Для этого будем
двигаться в сторону, обратную градиенту. Градиент — направление, в котором
достигается наибольший прирост значений. Градиент вычисляется следующим
образом:
.
Чтобы подправить веса, нужно вычислить градиент и отнять вектор
какой-нибудь наперёд заданной длины:
.
В данном случает подсчёт градиента будет выглядеть следующим
образом:


