38
где
= 50 Гц
– частота в ЭС;
∆
– величина небаланса в
ЭС; – коэффициент крутизны статической частотной
характеристики ЭС.
Второе отличие
заключается в том, что объединение
ЭС приводит к возрастанию абсолютных величин
нерегулярных
колебаний
обменной
мощности.
Максимальную передаваемую мощность (
) по
межсистемным связям рекомендуется определять в
соответствии с выражением (6) [2]. В ЭС, в отличие от
межсистемной связи, важна величина потребления
активной мощности. Её принято определять в соответствии
с выражением (7) [4], которое является аналогом
выражения (6).
Выражение (7) основа статистического метода расчета
электрической нагрузки в ЭС.
=
пр
− ∆
,
(6)
где
пр
–
предел
статической
устойчивости
электропередачи, МВт.
н
̂
=
н
̅
± ∙
√ (
н
)
н
,
(7)
где
̂
– расчетная величина нагрузки, МВт;
̅ = (
н
)
– математическое ожидание нагрузки, МВт;
– коэффициент надежности расчета (коэффициент,
определяющий вероятность превышения значения
расчетной нагрузки, для точности расчета
±10%
, что
соответствует погрешности инженерных расчетов,
значение коэффициента
= 1,0
);
(
н
)
– дисперсия
нагрузки, МВт2.
В период с 1959 по 1961 год Б.С. Мешель совместно с
Б.В. Гнеденко исследовали проблему рационального
расчета электрических нагрузок. В 1961 году в работе [5]
Б.В. Гнеденко изложил теоретико-вероятностные основы
статистического метода расчета электрических нагрузок. В
его основе лежит следующее предположение: мощность
единичного электроприемника
н
( )
, потребляемая в
момент времени , изменяется случайным характером.
Следовательно,
н
( )
является случайной функцией, а
( )
(8) случайная функция особого рода: она представляет
собой сумму случайных функций [4].
( ) = ∑
н=1 н
( )
(8)
При максимальном использовании экспериментальных
данных в математической статистике существует правило:
если случайная величина
(
н
)
нормально распределена с
плотностью распределения (9) и её параметры A и σ
неизвестны (итоги независимых наблюдений над
значениями величины
н
дали результаты
1
,
2
, . . . ,
), то
наилучшие оценки A и σ определяются по выражениям (10)
и (11) соответственно [5].
(
н
) =
1
∙ √2
∙
−
( − )
2
2∙
2
(9)
≈
1
∙ ∑
н=1 н
= ̅
(10)
≈ √
1
∙ ∑
н=1
(
н
− ̅ )
2
= √ (
н
)
(11)
III.
С
ТАТИСТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ
ДАННЫХ
Применяя вышеизложенное при статистической
обработке экспериментальных данных по потреблению ЭС
Калининградской области (КО) за 2019-2021 года
установлено, что независимые наблюдения величины
потребления нормально распределены с плотностью
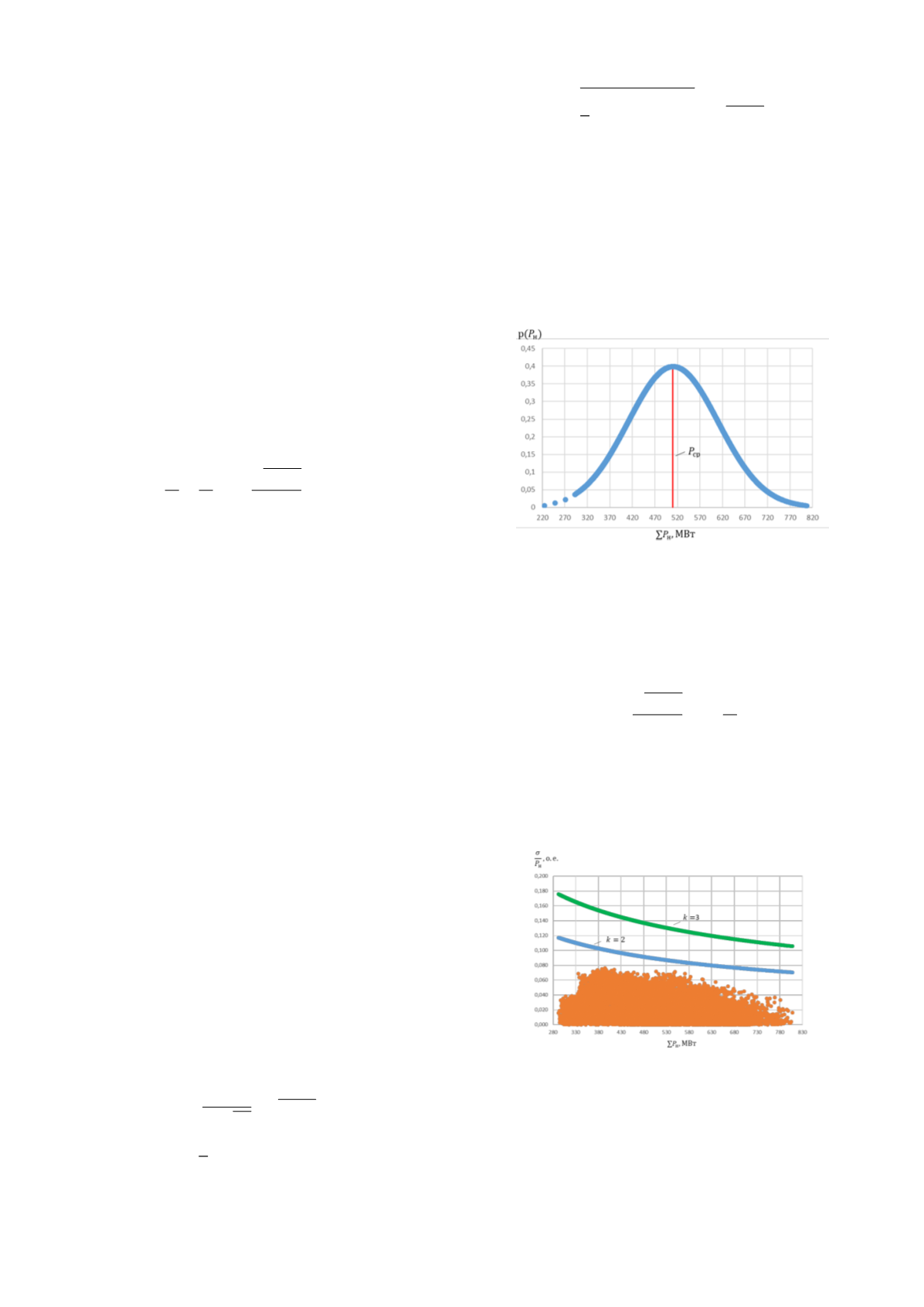
распределения (9) (рис. 1).
Рис. 1 – Нормальный закон распределения экспериментальных
данных по потреблению в ЭС КО за 2019-2021 года
Следовательно, для определения фактических значений
нерегулярных отклонений мощности и динамической
погрешности регулирования баланса мощности (
факт
)
(флуктуаций или нерегулярных колебаний мощности) (12)
можно применить метод статистического анализа данных.
факт
= ∙
√ (
н
)
н
= ∙
н
,
(12)
Используя метод статистического анализа данных
определены фактические флуктуации в ЭС КО за 2019-
2021 года (рис. 2). Применяя аппроксимационный метод
определена допустимая область фактических флуктуаций
(рис. 2).
Рис. 2 – Фактические флуктуации в ЭС КО за 2019-2021 года
Общий вид кривой, ограничивающей максимальные
колебания нагрузки, приведен в выражении (13). Значения
коэффициента надежности для точности расчета ±10%,
что соответствует погрешности инженерных расчетов,
принято равным
1,0
[6].


