26
2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТИ
Основные статистические понятия рассмотрим на примере подбрасывания
монеты в 2 копейки. При этом выпадение «герба» обозначим 0 коп., а «цифры» - 2
коп. Число подбрасываний обозначим буквой
n
. Так как есть всего 2 возможности,
то по теории вероятности в 50% случаев будет выпадать 0 коп., а в 50% - 2 коп. за
каждые два подбрасывания в среднем будет выпадать 0+2 коп.=2 коп., или в сред-
нем на одно подбрасывание 2 коп./2=1 коп. и тогда за
n
подбрасываний мы будем
набирать в среднем 1 коп.·
n=n
коп. этот результат довольно очевиден. Если мы
обозначим среднюю набранную сумму
N
(черта сверху означает «среднее»), то
получим
nN
=
(в данном примере).
В действительности же, если мы начнем подбрасывать монету, то навер-
няка окажется, что набранная сумма денег не точно совпадает с
nN
=
. На-
пример, может оказаться, что при
n
= 6 подбрасываний нуль выпадает 4 раза,
а 2 коп. – всего 2 раза, т.е. набранная сумма равна
N
= 2 коп. 2 = 4 коп.,
вместо ожидаемых
.
n N
коп6
==
Отклонение от среднего составило
.
.
.
NnNN
коп2 коп4 коп6
= − = −=
−
Как правило, в физике за меру отклонения результатов отдельных испы-
таний от среднеарифметического из результатов всех испытаний принимают
среднеквадратичное отклонение (или, что то же самое, среднеквадратичную
погрешность).
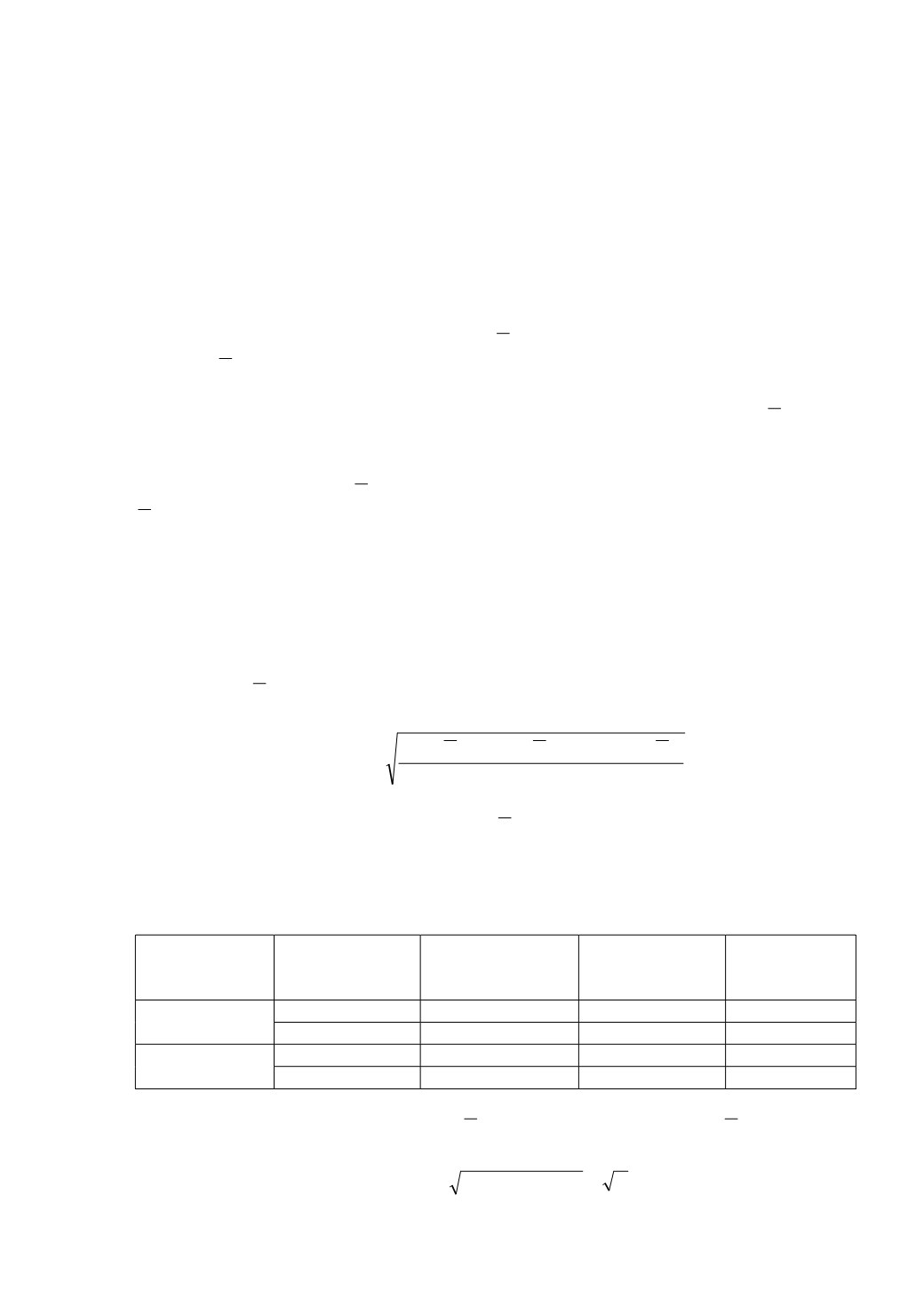
Среднеквадратичное отклонение определяется так: пусть число испыта-
ний равно n и пусть
N
1
, N
2
, N
3
, ... , N
n
числа, полученные в каждом испыта-
нии. Пусть
N
- среднее значение измерений величины (среднеарифметиче-
ское). Тогда среднеквадратичное отклонение Δ
N
равно
(
) (
)
(
)
n
N N ....
N N NN N
n
2
2
2
2
1
− + + − + −
=∆
.
Рассмотрим пример. Пусть
n
= 2, т.е. мы подбрасывали монету 2 раза
подряд. Ожидаемое среднее значение
.
n N
коп2
==
в каждой серии подбрасы-
ваний. Если выпадение 0 и 2 коп. равновероятно, то ожидаемые результаты
показаны в табл. 2.
Таблица 2
1-е подбрасы-
вание
2-е подбрасы-
вание
Возможность
Сумма денег
на два подбра-
сывания
Квадрат от-
клонения от
среднего
0
0
1-я
0 +0 = 0 =
N
1
( 0 – 2 )
2
= 4
2
2-я
0 +2 = 2 =
N
2
( 2 – 2 )
2
= 0
2
0
3-я
2 +0 = 2 =
N
3
( 2 – 2 )
2
= 0
2
4-я
2 +2 = 4 =
N
4
( 4 – 2 )
2
= 4
Вычислим среднее значение:
(
)
N n
N
====÷ +++ =
2
2 4 4220
, как и ожи-
далось. Среднеквадратичное отклонение:
(
)
.
/
N
2 4 4004
= +++ =∆


