33
Разряд необходимо прекратить,
иначе следующая ядерная частица не
будет отмечена в счетчике «своим» раз-
рядом. Для этого в цепь счетчика вво-
дится большое сопротивление порядка
10
9
Ом. До начала разряда напряжение в
точке
А
равно
U
0
(рис. 21). Ток разряда
I
,
вызванный влетевшей частицей, пони-
жает напряжение нити
U
A
= U
0
– IR
. Когда
U
A
падает ниже напряжения зажи-
гания, разряд прекращается. Через некоторый промежуток времени (
,CR
′
=τ
где
C
′
- емкость цепи) напряжение на счетчике восстанавливается, и счетчик
вновь готов к работе. Гасящее сопротивление выбирается таким образом,
чтобы потенциал нити был мал до тех пор, пока
положительные ионы не нейтрализуются. Счет-
чики Гейгера – Мюллера с внешним большим
гасящим сопротивлением называются несамога-
сящимися. Импульс, выходящий со счетчика,
имеет сравнительно большую величину, не нуж-
дается в усилении, его можно посмотреть на эк-
ране осциллографа или направить на пересчет-
ный прибор для счета (рис. 22).
Разряд в счетчике можно прекратить без помощи внешнего большого
сопротивления путем добавки «гасящего» газа. Такими газами являются па-
ры спиртов или галогены. Молекулы подобных газов поглощают излучение,
возникшее в результате нейтрализации положительных ионов, ответственное
за то, что разряд продолжается и продолжается. Молекулы спирта, «хватая»
это «лишнее» излучение, распадаются, поэтому спиртовой счетчик «стареет».
В галогенном счетчике молекулы Cl
2
или Br
2
тоже диссоциируют, но в ре-
зультате последующих рекомендаций их число почти сохраняется. Такие
счетчики с примесями газов называют самогасящимися.
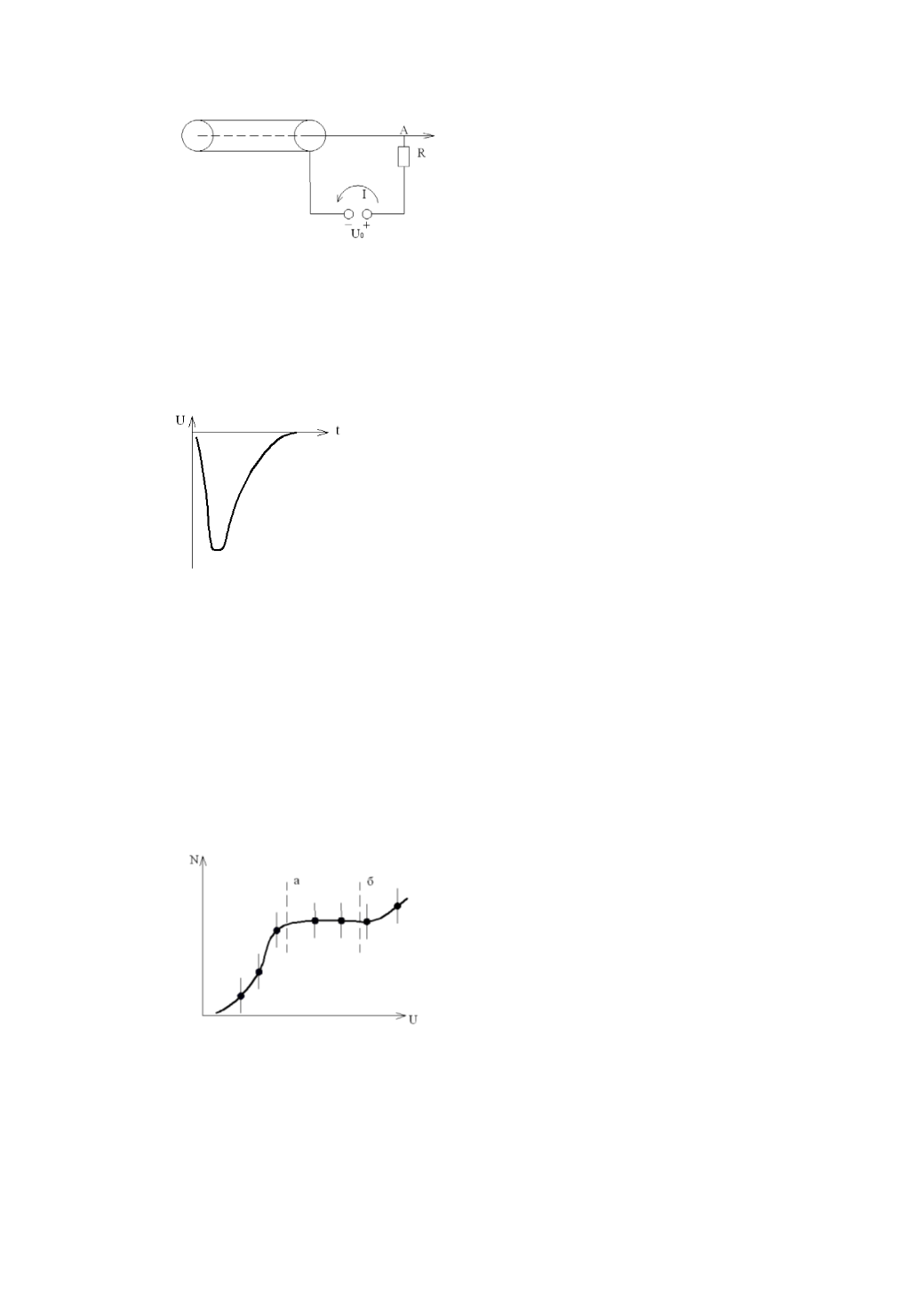
Важными характеристиками счетчика
Гейгера – Мюллера кроме величины рабо-
чего напряжения, стабильности работы и
величины выходного импульса являются
также рабочая область – «плато» и эффек-
тивность (рис. 23). Рабочая область хоро-
шо видна на счетной характеристике счет-
чика. Для снятия этой характеристики при
постоянном ядерном излучении повышают
напряжение на счетчике и считают число импульсов
N
, пришедших со счет-
чика за одинаковые промежутки времени. На графике
N(U)
можно сразу уви-
деть, есть ли «плато» и какова его протяженность. Хороший счетчик имеет
большой горизонтальный участок – плато, тогда какие–либо изменения на-
пряжения не окажутся на экспериментальных данных.
Рис. 21
Рис. 22
Рис. 23


