36
средних и алгоритма DBSCAN (Density-Based Spatial
Clustering of Applications with Noise).
При
реализации
алгоритмов
использовалась
полученная из открытых источников [10] информация о
потреблении электроэнергии (с декабря 2016 года по
январь 2018 года) высотного жилого здания в кампусе в
Бомбее. Здание состоит из 60 квартир, каждая из
которых оснащена интеллектуальным прибором учёта,
регистрирующим данные с частотой 60 минут.
A.
Иерархическая кластеризация
Особенность
иерархической
кластеризации
заключается в использовании подтвердившегося при
проведении
исследования
предположении,
что
потребители, подключенные к одной и той же фазе,
имеют высокую корреляцию между значениями
действующего напряжения, измеренными за некоторые
промежутки
времени.
Поэтому
устанавливать
взаимосвязь между величинами напряжения в различных
частях электрической цепи следует с помощью взаимной
корреляции: чем сильнее связь между переменными, тем
выше
коэффициент
корреляции.
Алгоритм
идентификации
фаз
на
основе
иерархической
кластеризации корреляционной матрицы выполняется по
следующему плану: сначала строится корреляционная
матрица между показаниями значений напряжения,
полученных со всех интеллектуальных приборов учета.
Для вычисления коэффициентов корреляции была
реализована программа, составленная на языке
программирования python, в которой была использована
функция corr из библиотеки pandas. Данная функция
предназначается
для
нахождения
коэффициента
корреляции Пирсона между переменными. Затем
выполняется иерархическая кластеризация полученной
корреляционной
матрицы.
Анализ
результатов,
полученных с помощью иерархической кластеризации,
показал, что алгоритм разделил данные на три кластера,
соответствующие трём фазам (цвета на рисунке –
зеленый, красный и голубой), в которых 26 из 30
значений напряжения фаз были верно отнесены к своей
фазе.
Результат
выполнения
алгоритма
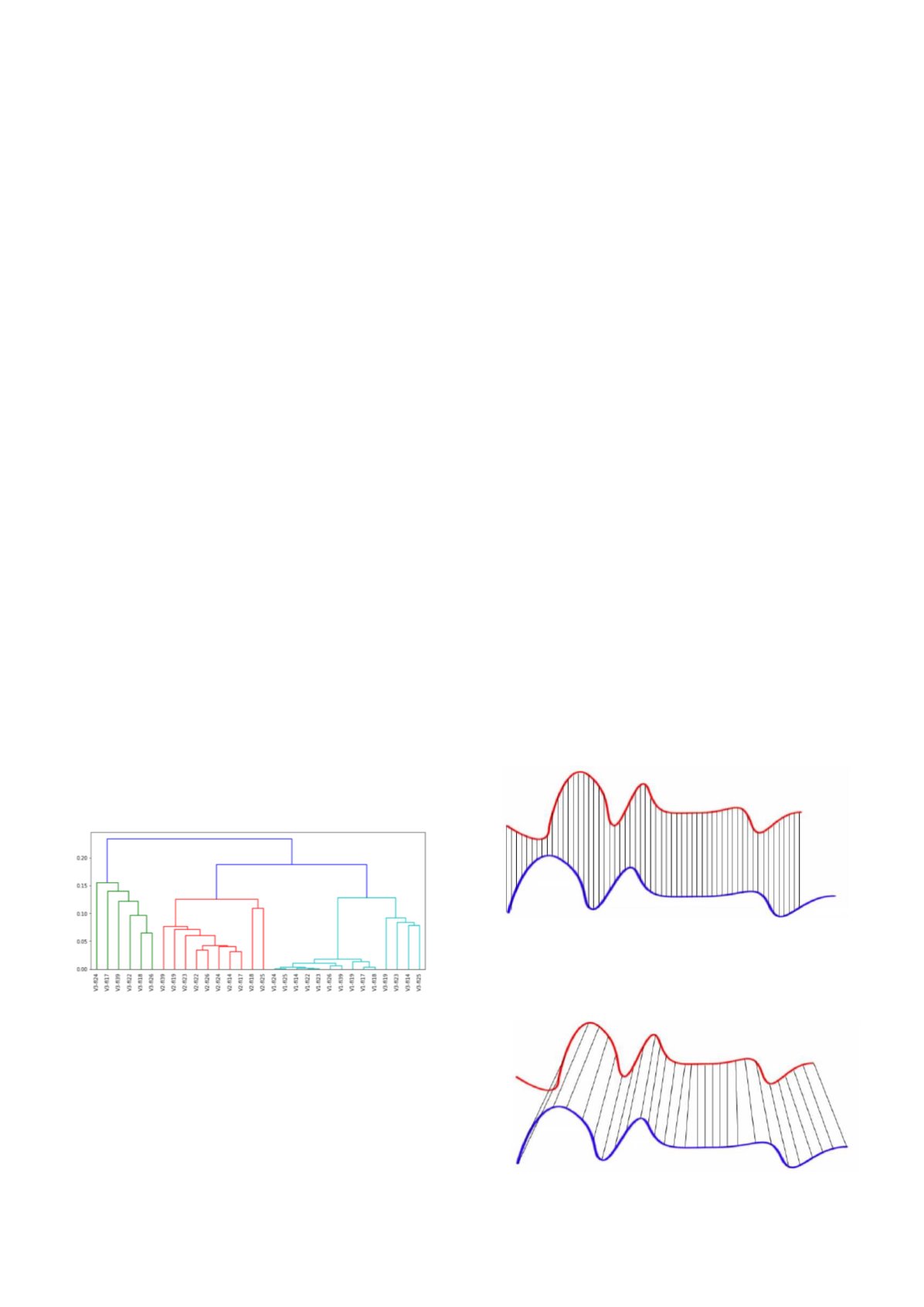
продемонстрирован на “Рис. 2”. Таким образом, точность
полученного алгоритма составила около 87 %.
Рис.2 – Результат иерархической кластеризации коэффициентов
взаимной корреляции действующих значений напряжений в местах
установки интеллектуальных приборов учета
При значительном увеличении объема выборки (7316
против 800 в исследуемом наборе) алгоритм
идентифицировал фазы со 100 % точностью.
B.
Метод k-средних
Основой алгоритма идентификации фаз может также
являться наиболее популярный способ кластеризации –
метод k-средних. Алгоритм на основе метода k-средних
заключается в формировании кластеров посредством
разбиения данных на k групп и последующей
минимизации суммарного квадратичного отклонения
точек кластеров от центров этих кластеров.
Однако при реализации алгоритма на основе данного
метода необходимо учесть, что центры кластеров,
созданные
посредством
метрики
евклидового
расстояния, используемой в стандартных алгоритмах
кластеризации, не отражают форму ряда. Такая мера
расстояния не подходит для временных рядов, так как
она не учитывает возможные временные сдвиги данных.
То есть, если два временных ряда сильно коррелированы,
но один из них сдвинут хотя бы на один временной шаг,
метрика евклидового расстояния будет ошибочно
считать их как далёкие друг от друга.
Для исследования алгоритма была составлена
программа, в которой использовались функции из
библиотеки sklearn, применяемой для решения
большинства задач машинного обучения. Реализация
алгоритма кластеризации на основе метода k-средних с
метрикой евклидового расстояния показала результат
менее точный, чем при выполнении иерархической
кластеризации: верно было определено 25 фаз из 30, что
составило около 83%. Тем не менее, существуют
исследования [9], в которых были получены результаты с
гораздо более высокой точностью при использовании
метода k-средних. Это обусловлено использованием
метрики для сравнения временных рядов вместо метрики
евклидового расстояния.
Поэтому следующим шагом в исследовании метода k-
средних было использование метрики динамической
деформации времени для сравнения серий (DTW –
Dynamic Time Warping). Данная метрика учитывает
сходства
между
двумя
временными
последовательностями, которые могут не совпадать в
точности по времени, скорости или длине. Иллюстрация
различий между метрикой евклидового расстояния и
метрикой DTW приведена на “Рис. 3” и “Рис. 4”.
Рис.3 – Иллюстрация метрики евклидового расстояния
Основное
различие
метрик
заключается
в
выравнивании временных рядов, которое минимизирует
евклидово расстояние между выровненными рядами.
Рис.4 – Иллюстрация метрики DTW


