235
Сценарий тестирования при наличии гармоники во
входном сигнале согласно стандарту СО [1]
следующий:
( ) = ( ) +
( ) = cos(2
ном
+ δ) +
cos(2
ном
+ δ )
,
где
( )
—
гармоническая составляющая, причем
номера гармоник варьируются от 2 до 50.
Критериями проверки для класса УСВИ P, более
точного, но вместе с тем более дорогостоящего,
являются погрешность оценки частоты (FE ≤ 0,005
Гц) и специальный параметр, учитывающий
одновременно оценки амплитуды и фазы,
—
TVE
(TVE ≤ 1%).
Похожий сценарий приводится в условиях наличия
интергармонических помех. Согласно стандарту СО
тестовый сигнал представляется в виде:
( ) = ( ) +
( ) = cos(2
ном
+
δ) +
m
cos(2 + δ )
,
где
( )
—
интергамоническое колебания;
меняется в пределах
10 ≤
≤
и
≤
≤ 2
ном
с шагом в 5 Гц;
=
ном
+ /2
и
=
ном
− /2
,
=
/
ном
.
Критериями проверки соответствия погрешностей
измерений УСВИ:
- для класса М: TVE ≤ 1,3%, FE ≤ 0,01 Гц, RFE не
нормируется;
- для класса P: погрешности не нормируются.
В данной статье для оценки параметров векторов в
условиях гармонических и интерагмонических
составляющих
предлагается
разработанный
полупериодный алгоритм ДПФ (MHDFT – modernized
half-cycle DFT). Длина окна, в течение которого
происходит обработка данных, исходя из названия, -
половина периода промышленный частоты, 10 мс.
На
структурной схеме рис.1 показаны все действия,
необходимые при оценке параметров входного
сигнала при его искажении любой составляющей.
Так, в блоке 2 происходит формирование
специальных
коэффициентов,
которые
затем
используются
при
коррекции
интересуемых
параметров.
Заранее,
до
формирования
коэффициентов, корректные значения амплитуды и
частоты достигаются применением сглаживания,
которое усредняют колебательную погрешности
оценки данных параметров.
Финальные значения TVE, при оценке параметров
в
условиях
гармонических
составляющих,
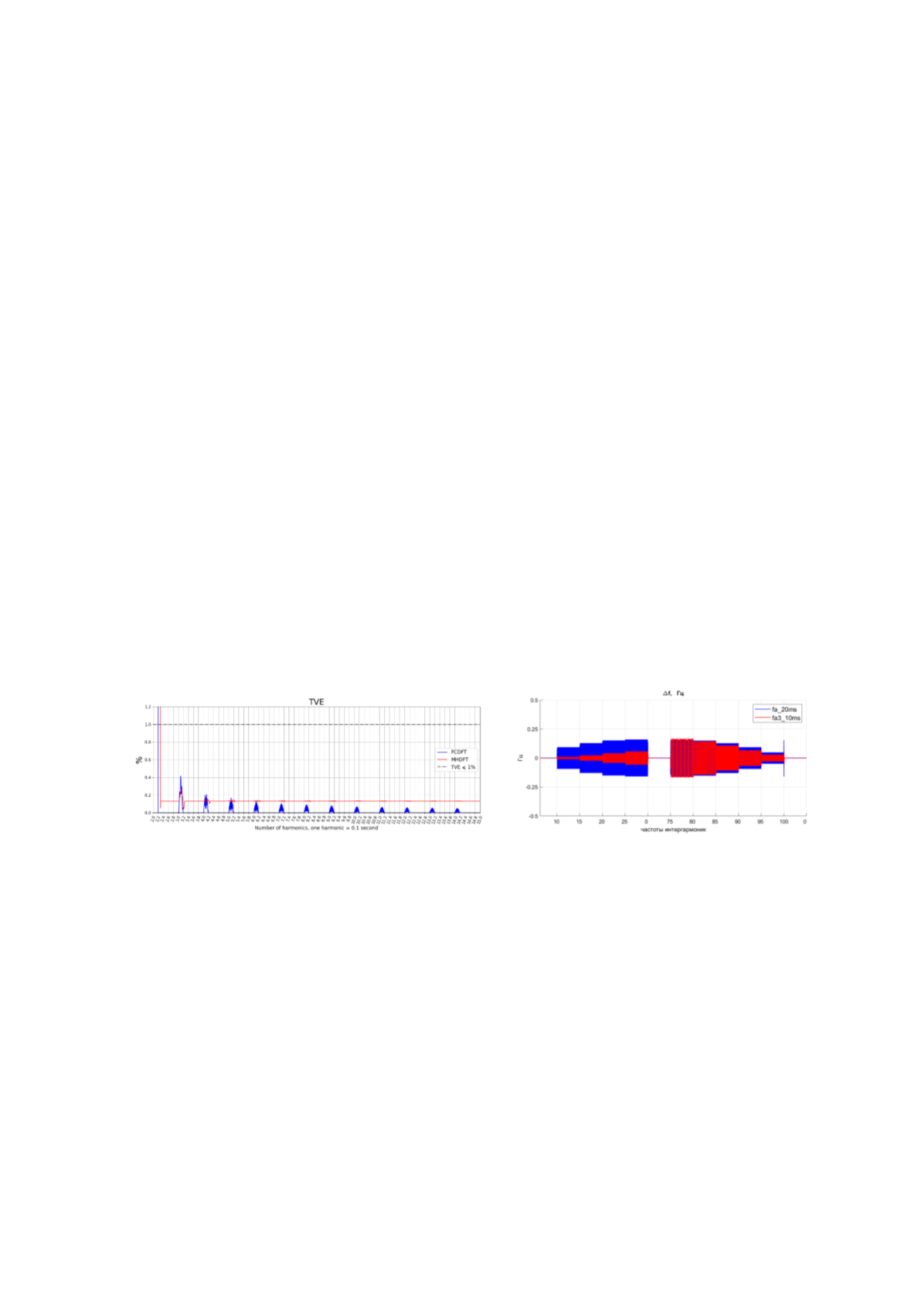
проиллюстрированы на рисунке 2. Видно, что
предлагаемый алгоритм позволяет оценить данный
параметр в допустимых пределах погрешностей,
которые требуются по стандарту [1], имея при этом
существенный запас.
Аналогично модернизированный полупериодный
алгоритм применятся для оценки частоты в условиях
интегармонических помех. На рис. 3 можно видеть,
что при приближении частоты интеграмоники к
частоте
номинального
сигнала
погрешность
увеличивается для обоих методов. Тем не менее за
счет увеличения времени обработки сигналов
последовательным сглаживанием колебательной
погрешности в модернизированном алгоритме
достигается более высокая точность оценки частоты.
III.
А
НАЛИЗ ПАРАМЕТРОВ ГАРМОНИЧЕСКИХ И
СУБГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ
Стоит
рассмотреть
возможность
оценки
гармонических составляющих при использовании
алгоритмов ДПФ полного и полупериодного цикла
при фиксированной частоте дискретизации.
На рисунке 4 представлены оценки амплитуды и
частоты полупериодным алгоритмом, MHDFT, при
частоте дискретизации 24 кГц. Видно, что при оценке
7, 9 и 11 гармоник наблюдаются синусоидальные
колебания вокруг соответствующих этим гармоникам
частот. Связано это с тем, что количество дискретных
отчетов на половину периода рассматриваемых
гармоник не укладывается целым числом в окно
алгоритма, в течение которого эти данные
накапливаются. Поэтому в данном случае так же, как
и было описано ранее для амплитуды и частоты,
применяется
последовательное
сглаживание:
дополнение к названию MHDFT “_s” обозначает
однократное сглаживание на одном полупериоде,
“_ss”
—
двукратное соответственно и так далее. Так,
существенного уменьшения ошибки оценки частоты,
менее пяти тысячной Герца, можно достигнуть уже
через 1.5 периода колебаний наблюдаемой гармоники
(MHDFT_ss), а оценки амплитуды, менее одной
тысячной от номинального значения, через период
(MHDFT_s).
Как было упомянуто ранее, Сертификационные
испытания УСВИ требуют получения заданной
точности
оценки
параметров
векторов
промышленной частоты, принимаемых на фоне
интергармоник. Интергармоники задаются на
частотах субгармонических колебаний. Задача
определения
параметров
субгармонических
Рис 2 – Оценка параметра TVE при искажении основного сигнала Рис 3 – Сопостовление качества оценки частоты фазного
напряжения гармониками c номерами n = 2
÷ 15
алгоритмами MHDFT (красные кривые) и FCDFT (синие)


