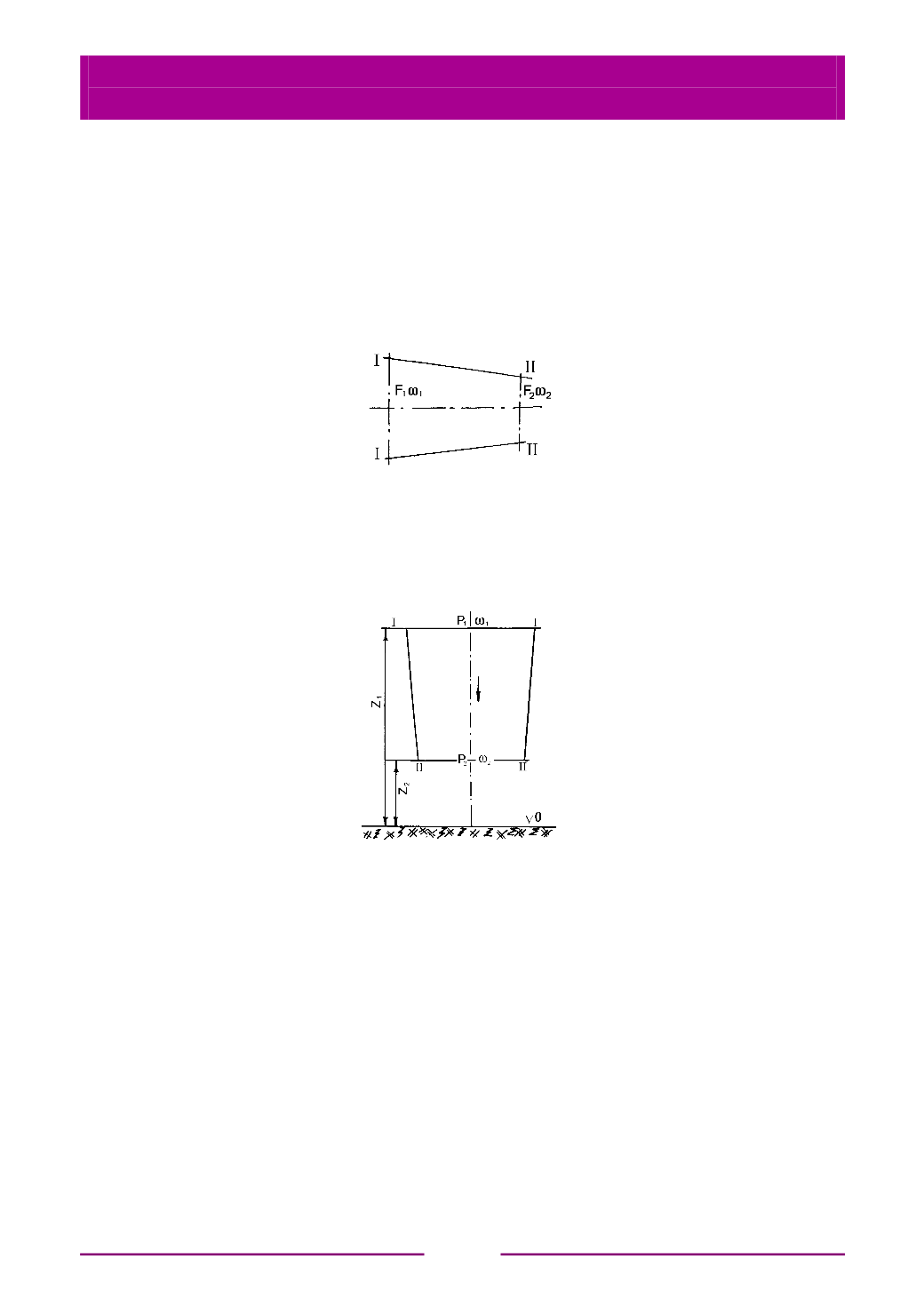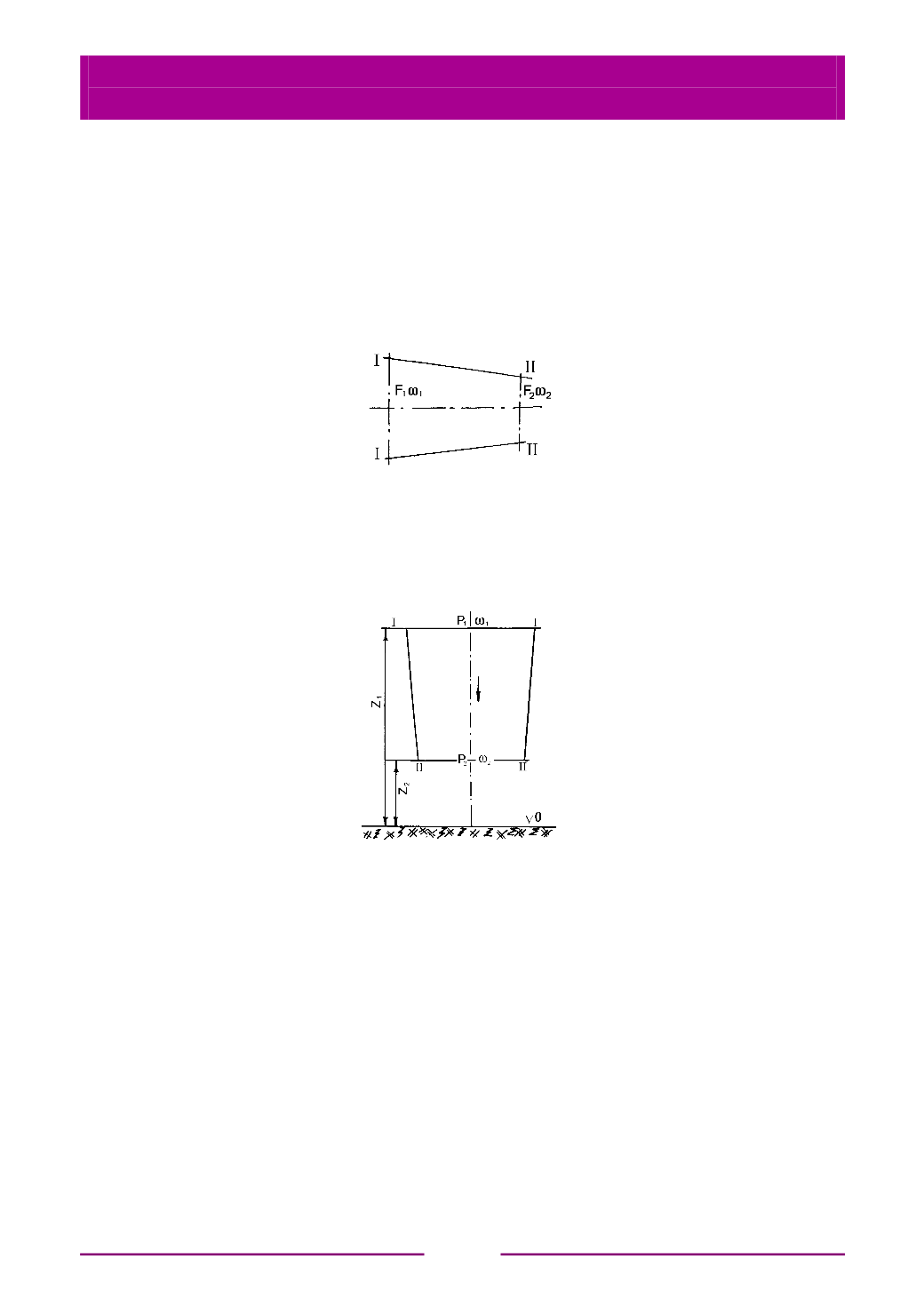
ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
50
V
1
=
V
2
и
F
1
ω
1
=
F
2
ω
2.
(3.19)
Отсюда следует, что в рассматриваемых условиях скорости потоков в каналах
обратно пропорциональны площадям сечений канала
ω
1
/
ω
2
=
F
2
/
F
1
.
При движении сжимаемой жидкости (газа) принцип равенства объемов
заменяется принципом равенства масс. Уравнение неразрывности приобретает
при этом следующий вид:
F
1
ω
1
ρ
1
=
F
2
ω
2
ρ
2
.
Рис. 3.4. Расчетная схема для вывода
уравнения Бернули
Уравнение Эйлера можно доказать разными способами. Ниже приводится
наиболее простой вывод, основанный на законе сохранения энергии (рис. 3.5).
Рис. 3.5. Расчетная схема для вывода
уравнения Эйлера
Рассмотрим два сечения I - I и II - II канала, в котором движется
идеальная жидкость (несжимаемая, без трения). Сечения расположены на
отметках
z
1
и
z
2
. Кинетическая энергия, отнесенная к одному м
2
, в сечении I-I
при скорости
ω
1
равна
2/
2
1
ρω
.
Размерность этой величины [м
2
/с
2
] [кг/м
3
] = [Н
⋅
м/м
3
] = [Дж/м
3
].
Потенциальная энергия давлений
Р
1
и
Р
2
имеет размерность
[Н/м
2
] = [Н
⋅
м/м
3
] = [Дж/м
3
].
Потенциальная энергия положения в сечениях I - I и II - II соответственно
равна
gz
1
ρ
1
и
gz
2
ρ
2
при следующей размерности:
[м/с
2
] [ м ] [кг/м
3
] = [Н
⋅
м/м
3
] = [Дж/м
3
].