Теплофизика и основы металлургической теплотехники - page 50

ТЕПЛОФИЗИКА И ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ
ТЕПЛОТЕХНИКИ
48
Для любой выделенной части поверхности, находящейся в равновесии,
поверхностные силы перпендикулярны к поверхности и направлены внутрь ее.
Дальнейшие выводы остаются в силе как для несжимаемой жидкости, так
и для газов при малых давлениях. Для вывода уравнения равновесия
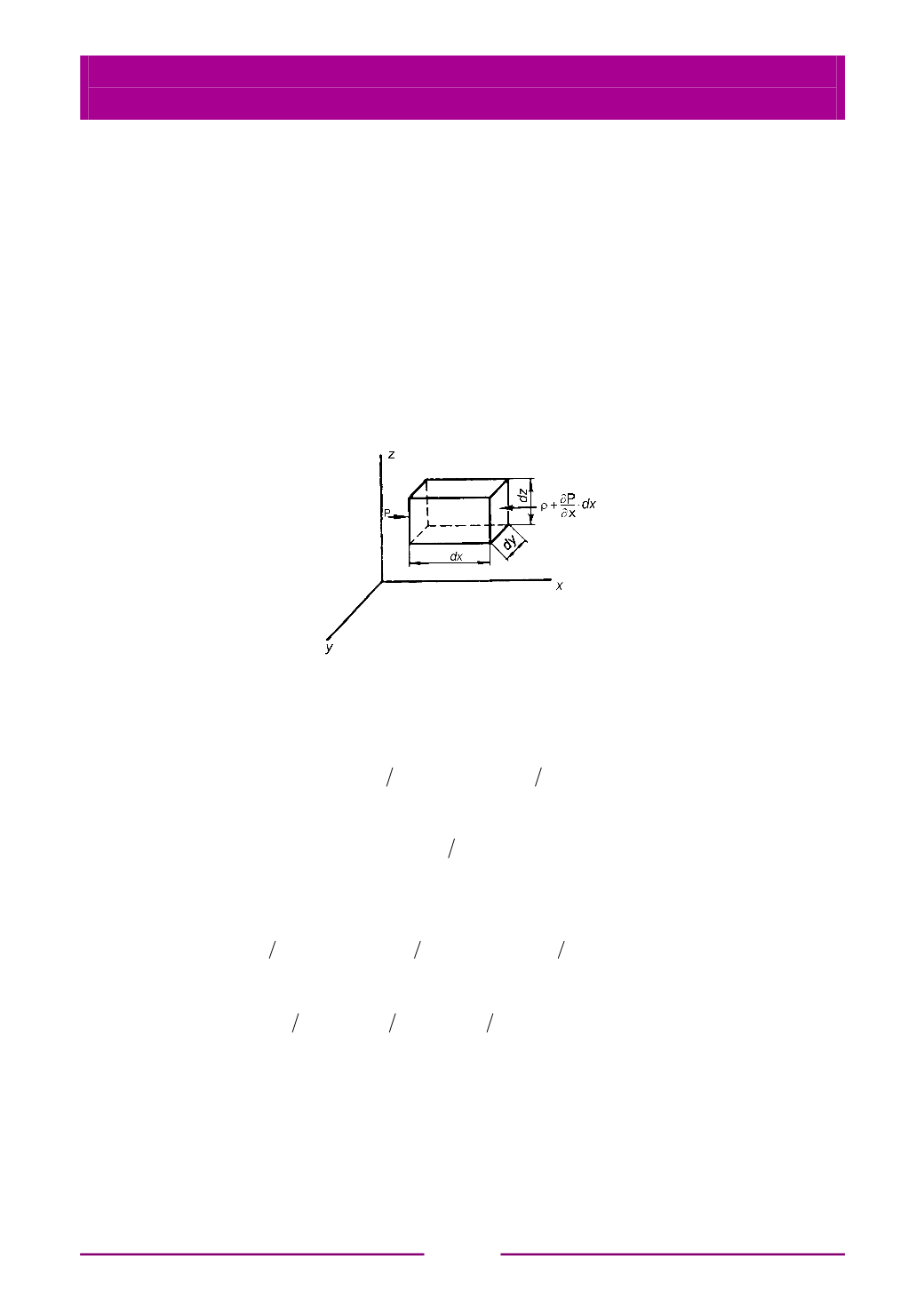
выделим элементарный параллелепипед с ребрами dх, dy , dz и объемом
dV = dx dy dz . На параллелепипед действуют силы тяжести и давления на
каждую из граней (рис. 3.3).
Обозначим проекции ускорения силы тяжести на оси координат
через gx, gy, gz. Проекций самой силы тяжести будут равняться соответственно:
gx⋅ρ⋅dV, gy⋅ρ⋅dV, gz⋅ρ⋅dV (ρ - плотность газа). Эти силы должны быть
уравновешены разностью давлений, приходящейся на соответствующие грани.
Рис. 3.3. Схема сил, действующих на элементарный объем
в условиях равновесия
Для грани, перпендикулярной оси x равнодействующая сил давления равна
( ) [ ] x PdV dydz dxxP P P ∂ ∂−= ∂∂+ − , (3.12)
а сумма сил, действующих в направлении оси x ,
0 =∂ ∂− x PdV dV g
x ρ . (3.13)
Рассуждая аналогично, получим условия равновесия для всех трех осей
координат.
0 ,0 ,0 =∂ ∂− =∂ ∂− =∂ ∂− z P g y P g x P g z
y x ρ ρ ρ .
Если направить силу тяжести по координате z, то
. ,0 ,0 ρ g zP yP xP −=∂ ∂ =∂ ∂ =∂ ∂
Интегрируя последнее уравнение, получим
C + −= zg P ρ . (3.14)
Постоянную интегрирования С определяют для сечения z0 , в котором газ
соприкасается с атмосферой. Подставляя z = z0 и принимая Р = Ро ,
получим С = Р + gρz0. Окончательно имеем