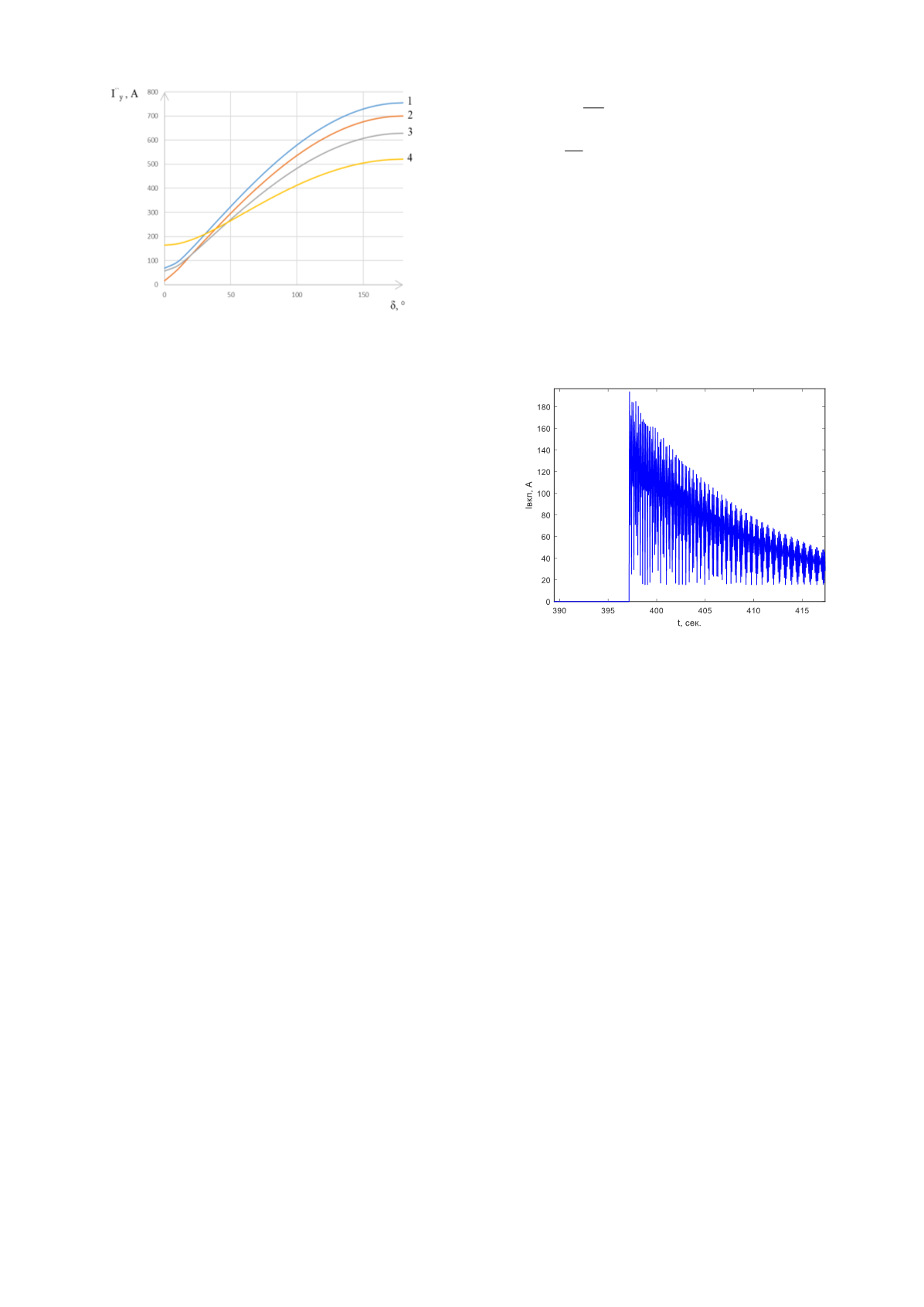
195
Рис. 1 – Зависимость уравнительного тока от угла δ и
i
f
(1 –
i
f
= 17,5 А, 2 –
i
f
= 10 А, 3 –
i
f
= 6 А, 4 –
i
f
= 3 А)
Очевидно, что наименьший уравнительный ток будет
иметь место в случае, когда ЭДС генератора полностью
совпадает по амплитуде с напряжением ЭЭС, а также при
δ, равном 0 °, что соответствует идеально выполненному
способу точной синхронизации. Однако, улавливание
момента, когда угол δ близок к 0 °, может затянуть процесс
синхронизации. Промежуточный метод синхронизации
выступает некой модернизацией традиционного способа
ТС, при этом предлагается расширить допустимый
диапазон угла δ, а для предотвращения больших
уравнительных токов в момент включения агрегата —
снизить ток, подаваемый в обмотку возбуждения. Согласно
проведенным расчётам для исследуемого генератора,
рекомендуется включение агрегата на параллельную
работу при угле δ, лежащем в диапазоне 30 – 40 °, и токе
возбуждения от 10 А до 6 А: в этом случае значение
уравнительного тока соответствует около 80 % от
максимального уравнительного тока при традиционном
методе самосинхронизации. То есть модернизированный
метод синхронизации является целесообразным в
использовании,
позволяя
уменьшить
величину
уравнительного тока в момент включения и выполнить
процесс быстрее, чем при использовании способа точной
синхронизации.
III.
М
АТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ИССЛЕДОВАНИЯ
РАЗЛИЧНЫХ ВАРИАНТОВ СИНХРОНИЗАЦИИ
Для упрощения исследования различных вариантов
синхронизации разработана математическая модель
процесса
включения
исследуемого
генератора
электростанции НГТУ на параллельную работу с системой
в среде MATLAB. Основная задача модели – графическая
визуализация всех возможных вариантов синхронизации в
виде зависимости уравнительного тока и угла δ от времени
(Рис. 2). Данная математическая модель даёт возможность
на основании графического представления выбрать
условия, являющиеся оптимальными для последующей
синхронизации
генератора
и
обеспечивающими
минимальное значение уравнительного тока в момент
включения.
Основу функционирования математической модели
составляют уравнения, описывающие электромагнитные и
электромеханические процессы, имеющие место при
синхронизации машины с сетью. Они образуют систему
двух дифференциальных уравнений в соответствии с
выражением (2).
Т
С
синхр
р
Г
С
ω
М М М М ,
,
δ
ω ω .
d
J
dt
d
dt
= − −
−
= −
(2)
где
J
−
момент инерции ротора исследуемого
генератора, М
Т
−
момент турбины, М
С
– момент
сопротивления, М
синхр
– синхронный момент, М
р
–
реактивный момент, ω
Г
– частота вращения исследуемого
генератора, ω
С
– частота вращения эквивалентного
генератора системы.
Использование модели заключается в варьировании
начальных условий, предшествующих включению
генераторного выключателя. В качестве них выбран
момент включения в секундах, он определяет угол δ.
Рис. 2 – Изменение уравнительного тока во времени при
использовании промежуточного модернизированного метода
Исследование
на
математической
модели
традиционного метода точной синхронизации позволило
получить величину уравнительного тока в момент
включения, равную 65 А, при использовании метода
самосинхронизации — 700 А, при использовании
модернизированного метода (Рис. 2) — 194 А.
Промежуточный метод позволил добиться токов в момент
включения в 3,6 раза меньше даже в худшем случае, когда
угол δ в момент включения достиг своего максимального
возможного значения (40 °), чем при традиционном методе
самосинхронизации, но почти в 3 раза больше, чем при
использовании
метода
точной
синхронизации.
Полученные
на
модели
данные
подтверждают
аналитический расчёт и целесообразность использования
промежуточного
модернизированного
метода,
осуществляющего процесс синхронизации быстрее, чем
способ ТС. Следует отметить, что уравнительный ток не
превышает величину трехфазного короткого замыкания и
как видно из математической модели, генератор успешно
втягивается в синхронную работу.
IV.
А
ВТОМАТИЧЕСКОЕ УСТРОЙСТВО
СИНХРОНИЗАЦИИ
Для автоматической синхронизации генераторов на
базе учебной электростанции НГТУ разработан
микропроцессорный синхронизатор. Цифровое устройство
представляет
собой
подсистему
комплекса
микропроцессорной противоаварийной автоматики КПА–
М, поскольку это является выгодным экономическим
решением в рамках площадки проведения экспериментов.


